

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
SEP-120 -- TABLE OF CONTENTS
Inversion
3-D subsalt imaging via regularized inversion with model preconditioning (ps.gz 6817K) (pdf 2289K) (src 24567K)
Clapp M. L. and Clapp R. G.
Subsalt imaging is a difficult but increasingly important problem.
The poor illumination that occurs when seismic energy is affected
by the complex subsurface at and around salt bodies causes significant
shadow zones in migration results. These shadow zones may contain
real signal, but it is weak compared to the artifacts caused by multipathing
and poor illumination. To reduce artifacts and recover this energy,
thereby improving the image, we use an imaging (migration) operator
in a regularized least-squares inversion. The regularization operator
acts on the offset ray parameter (reflection angle) axis of the model space.
Performing several iterations of regularized inversion that penalize large
changes along the offset ray parameter axis results in an image
with recognizable events in the shadow zones and fewer artifacts.
We perform regularized inversion with model preconditioning on real
2-D and 3-D data to obtain seismic images that are better in poorly
illuminated areas than migration results.
Target-oriented wave-equation inversion (ps.gz 200K) (pdf 330K) (src 835K)
Valenciano A. A., Biondi B., and Guitton A.
A target-oriented strategy can be applied to estimate the wave-equation least-squares inverse image (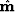 ) by explicitly computing the Hessian (
) by explicitly computing the Hessian (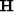 ).
The least-squares inverse image is obtained as the solution, using a conjugate gradient algorithm, of a non-stationary least-squares filtering problem
).
The least-squares inverse image is obtained as the solution, using a conjugate gradient algorithm, of a non-stationary least-squares filtering problem 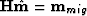 (where
(where 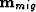 is the migration image, and the rows of the Hessian are non-stationary filters).
This approach allows us to perform the number of iterations necessary to achieve the convergence, by exploiting the sparsity and structure of the Hessian matrix. The results on a constant velocity model and a model with a velocity Gaussian anomaly show the validity of the method.
is the migration image, and the rows of the Hessian are non-stationary filters).
This approach allows us to perform the number of iterations necessary to achieve the convergence, by exploiting the sparsity and structure of the Hessian matrix. The results on a constant velocity model and a model with a velocity Gaussian anomaly show the validity of the method.
Inversion and fault tolerant parallelization using Python (ps.gz 102K) (pdf 159K) (src 172K)
Clapp R. G.
Many current areas of research at SEP involve large-scale inversion problems
that must be parallelized in order to be tractable.
Writing fault-tolerant, parallel code requires
significant programming expertise and overhead.
In this paper, a library, written in Python, is described that
effectively simulates a fault-tolerant parallel code,
using simple serial programs.
In addition, the library provides the
ability to use these parallel objects in
out-of-core inversion problems in a fault-tolerant manner.
Anisotropy
Imaging steeply dipping reflectors in TI media by wavefield extrapolation (ps.gz 5564K) (pdf 619K) (src 26978K)
Shan G. and Biondi B.
We develop an anisotropic plane-wave migration method based on wavefield extrapolation.
In this new scheme, we decompose both source and receiver wavefields into plane waves by delaying
shots. For each plane wave, we design a tilted coordinate system whose tilting angle depends on
the propagation direction of the plane wave. The wavefield extrapolation is done by an implicit isotropic operator
plus an explicit anisotropic correction operator. We apply this method on a synthetic dataset.
The results show that our scheme can accurately handle overturned waves and image steeply dipping reflectors
in transversely isotropic media with a vertical axis of symmetry (VTI).
Angle-domain common image gathers for anisotropic migration (ps.gz 804K) (pdf 648K) (src 1841K)
Biondi B.
I present a general methodology for computing and analyzing
Angle Domain Common Image Gathers (ADCIGs) in conjunction with anisotropic
wavefield-continuation migration.
I demonstrate that the aperture angles estimated by transforming
prestack images using slant stacks along the subsurface-offset axis
are a good approximation of the phase aperture angles,
and that they are exactly equal to the phase aperture angles
for flat events in VTI media.
I introduce a generalization of the concept of migration impulse response
for the computation of prestack images function
of the subsurface offset that enables a straightforward
analytical analysis of the reflector movements
caused by perturbations in anisotropic parameters.
This analysis shows that the Residual Moveout (RMO)
in migrated ADCIGs is function of both the
phase aperture angle and the group aperture angle.
The dependency of the RMO function on
the group angles adds some complexity to the RMO
analysis because the computation of group angles
from phase angles, which are measured from the ADCIGs,
depends on the local background anisotropic velocity
at the reflector point.
Several numerical examples demonstrate the accuracy
of the RMO function predicted by my kinematic analysis,
and in contrast, that the approximation of the group angles by the phase angles
may lead to substantial errors for events reflected
at wide aperture angles.
3D wavefield extrapolation in laterally-varying tilted (ps.gz 2088K) (pdf 843K) (src 7127K)
Shan G. and Biondi B.
We develop a new 3D wavefield-extrapolation method for a transversely isotropic (TI) medium with a
symmetry axis. The wavefield extrapolation is done by an implicit isotropic
extrapolation operator with an explicit correction operator. The explicit correction
is a 2D convolution operator in the space domain,
whose coefficients are estimated by a weighted least-squares method in the Fourier domain.
The extrapolation operator is stable and suitable for laterally-varying 3D TI media.
This new method can be used to extrapolate wavefields in a 3D transversely isotropic medium
with a vertical symmetry axis (VTI) in tilted coordinates.
We also discuss the effects of the filter length on its accuracy and shorten the filter by
changing the least-squares weighting function.
We present the impulse response of our algorithm and compare it with the
anisotropic phase-shift method.
Common azimuth migration for elliptical and VTI media (ps.gz 66K) (pdf 129K) (src 69K)
Sen S. and Biondi B.
We derive the Commom Azimuth downward continuation operator for elliptically anisotropic and VTI media. For elliptically anisotropic media, the Common Azimuth downward continuation operator derived by a stationary phase approximation of the full 3-D downward continuation operator is exact and it agrees with the constraint imposed by the Common Azimuth approximation on the propagation direction of the source and receiver rays. For VTI media, the dispersion relationship is much more complicated and results in a quartic equation for the stationary path. We introduce a bounded form of Common Azimuth migration for this kind of media, which allows us to develop closed-form analytical solutions without directly solving the quartic equation. Error analysis indicates that the derived analytical solution has similar accuracy as that obtained by solving the full quartic equation. 3-D impulse responses of the anisotropic Common Azimuth downward continuation operator also show significant differences compared to the isotropic operator even at moderate propagation angles.
Automated interpretation
Update on flattening without picking (ps.gz 1762K) (pdf 812K) (src 49160K)
Lomask J., Guitton A., Fomel S., and Claerbout J.
We present a method for efficiently flattening 3D seismic data volumes. First local dips are calculated over the entire seismic volume. The dips are then resolved into time shifts using a Gauss-Newton iterative approach that exploits the Fourier domain to maximize efficiency. To handle faults (discontinuous reflections), we apply a weight inversion scheme. This approach successfully flattens a synthetic faulted model, a field salt peircement dataset, a field dataset with an angular unconformity, and a faulted field dataset.
Flattening without picking faults (ps.gz 232K) (pdf 141K) (src 10015K)
Lomask J., Guitton A., and Valenciano A.
We show that iteratively re-weighted least squares (IRLS) can flatten data cubes with vertically-oriented faults without having to pick the faults. One requirement is that the faults need to have at least part of their tip-lines (fault terminations) encased within the 3D cube. We demonstrate this method's flattening ability on a faulted 3D field data-set.
Non-linear estimation of
vertical delays with a quasi-Newtom method (ps.gz 1805K) (pdf 680K) (src 100593K)
Guitton A., Lomask J., and Fomel S.
A local dip (or step out) between two adjacent traces embeds the necessary
information to go from one reflection on one trace to the same
reflection on the next. In more dimensions, i.e., 3-D, the same result
is obtained between distant traces by integrating the local dips in all directions,
thus obtaining relative delay maps useful for (1) automatic full-volume
picking and (2) automatic flattening of horizons.
The estimation of these maps from local dips is a non-linear
process. In this paper, this problem is solved with a
quasi-Newton technique for 2-D slices and 3-D cubes. Furthermore,
the estimation of the relative delays is done globally in a least-squares
sense for all reflectors at once.
Synthetic and field data examples illustrate the ability
of the algorithm to flatten horizon according to their geological
time. As a natural extension of our algorithm, any horizon can also be
picked automatically at no additional cost.
Image segmentation with bounds (ps.gz 647K) (pdf 301K) (src 5210K)
Lomask J. and Biondi B.
Image segmentation Hale and Emanuel (2002, 2003); Shi and Malik (2000) for tracking salt boundaries Lomask et al. (2004); Lomask and Biondi (2003) is extremely memory intensive. Memory saving measures must be implemented in order to consider applying this technique to 3D seismic cubes. If coarse bounds can be picked, either manually or using another automatic algorithm, this image segmentation algorithm can then be used to partition between the bounds. Unfortunately, the quality of the segmentation result is strongly affected by the shape of the image. For example, elongated images are more likely to be partitioned along their shortest dimension.
In this note, we present one such memory saving technique and demonstrate its ability to pick a salt boundary on a 2D seismic section. By imposing bounds, we significantly reduce the size of the problem and, as a result, increase efficiency and robustness. Also, errors created by segmenting thin images can be rectified with novel boundary conditions described here.
...
Interpolation and amplitudes regularization
Data regularization: inversion with azimuth move-out (ps.gz 322K) (pdf 334K) (src 1337K)
Clapp R. G.
Data regularization is cast as a least-squares inversion problem.
The model space is a five-dimensional (t,cmpx, cmpy, hx, hy) hypercube.
The regularization minimizes the difference between various
(t, cmpx, cmpy) cubes by applying
a filter that acts in (hx,hy) plane. Azimuth Move-out is used
transform the cubes to the same ( hx,hy) before applying
the filter.
The methodology is made efficient by a Fourier-domain
implementation, and preconditioning the problem.
The methodology, along
with two approximations is demonstrated
on 3-D dataset from the North Sea.
The inversion result proves superior at a reasonable cost.
Interpolation and signal extraction of teleseismic wavefields with the linear radon transform (ps.gz 2365K) (pdf 917K) (src 46149K)
Wilson C. K. and Guitton A.
We present a new method for data interpolation and signal/noise separation of teleseismic wavefields recorded by regional seismic arrays. The method exploits the plane wave nature of direct arrivals and receiver-side arrivals from regional scale structure by decomposing the recorded wavefield into a plane wave basis using the linear radon transform. Casting the radon transform as an inversion problem allows the incorporation of time dependent weighting schemes and model variance tuning which are helpful in minimizing artifacts related to the transform process while enhancing lower amplitude arrivals. Following radon transformation, we mute portions of the radon panel that represent plane waves with significantly different moveout (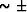 .1 s/km) relative to the direct arrival. Transformation back to the data domain from the muted radon domain gives the original signal without (1) plane waves following undesired moveouts, (2) white ambient noise, and/or (3) arrivals not represented well by plane waves (diffractions). Interpolation follows from the inverse data spray operation computed upon return to the data domain and the implicit assumption that a plane wave basis provides the most compact representation of the teleseismic wavefield.
.1 s/km) relative to the direct arrival. Transformation back to the data domain from the muted radon domain gives the original signal without (1) plane waves following undesired moveouts, (2) white ambient noise, and/or (3) arrivals not represented well by plane waves (diffractions). Interpolation follows from the inverse data spray operation computed upon return to the data domain and the implicit assumption that a plane wave basis provides the most compact representation of the teleseismic wavefield.
Focusing-effect AVO/AVA: overview of results and assessment of problems (ps.gz 1525K) (pdf 676K) (src 3174K)
Vlad I.
Small-scale heterogeneities in the Earth
produce visible focusing of seismic wavefield amplitudes with offset, but
minimal variations in traveltimes. These effects are called
Focusing-Effect AVO (FEAVO) or AVA (FEAVA) for avoiding confusion
with lithology-caused AVO/AVA. FEAVO/FEAVA is not an unpredictable
phenomenon that occurs at random. It appears in a number of
well-defined geological settings, it can be modeled with appropriate
precautions, it can be identified by its spatially predictable
patterns, and can be removed in a manner that takes into account the
specific physics involved. This paper summarizes work published over
the course of several years in seven different SEP reports, providing
an overview of the results obtained up to date and an assessment of
the most critical problems to be solved.
Interpolating with data-space prediction-error filters (ps.gz 1078K) (pdf 455K) (src 6362K)
Curry W.
The Madagascar sea elevation dataset presents a problem where data are
collected along crossing tracks. These tracks are not straight, and
are therefore irregular in the model space. Previous methods assumed that the
data were regularly sampled in the model space coordinate system, or
did not take into account the regularities in the acquisition of the data.
Instead of attempting to find a prediction-error filter in the model space,
I estimate two prediction-error filters in a coordinate system based
on the data's spatial distribution, and show how to
regularize the data with these filters with promising results. I
then show how this strategy can be applied to 2D and 3D land surveys
when data predicted by reciprocity is included.
Non-stationary PEFs and large gaps (ps.gz 421K) (pdf 390K) (src 1139K)
Curry W.
Prediction-error filters (PEFs) may be used to interpolate missing data, either
to increase the sampling of data that are regularly-sampled Spitz (1991),
as well as to interpolate larger gaps in data Claerbout (1992, 1999). In addition to
using multi-dimensional PEFs, non-stationary PEFs Crawley et al. (1998) have been used
to interpolate regularly-sampled data Crawley (2000). Non-stationary
...
Imaging
ADCIGs for forward-scattered wavefields (ps.gz 275K) (pdf 222K) (src 3479K)
Shragge J., Artman B., and Biondi B.
We extend the 2-D theory of angle-domain common-image gathers
(ADCIGs) to forward-scattered wavefields, and present a method for
extracting reflectivity as a function of either the reflected or
converted-wave
receiver-side scattering angle. We use the shot-profile
configuration of wave-equation migration along with planar source and
receiver wavefields to generate an analytic hyper-plane surface in
the intermediate offset-domain common-image gather space.
Geometrical relations and partial derivatives of
the hyper-plane function generate six constraint equations for the
the unknown six parameters, allowing us to solve for the source-
and receiver-side reflection angles and geologic dip angle.
Results of numerical experiments indicate that information on
wavefield focusing is present in forward-scattered ADCIGs, which suggests
that this algorithm may be useful tool for improving wave-equation
based tomography of transmission wavefields.
Time windowing passive seismic data in the frequency domain (ps.gz 115K) (pdf 137K) (src 245K)
Artman B.
One of the principle obstacles to the utility of passive seismic data
is its bulk. With several hundred to thousands of geophones, we are able
to generate mountains of data in a very short time. The simplest
method of trimming down this volume is to keep only the recorded
wavefield around times when usable source energy is known to be
present. In the case of teleseismic imaging, or when utilizing
unconventional, but known sources, this is easily done. However, if
one hopes to image with the truly ambient noise field, time windowing
amounts to removing needed signal.
...
Converted-wave common-azimuth migration (ps.gz 384K) (pdf 491K) (src 682K)
Rosales D. A. and Biondi B.
Multicomponent seismic data may hold a wealth of information
for oil exploration and
reservoir characterization. Multicomponent seismic contains energy
from converted waves that is not seen in
conventional seismic; therefore, the development of new
techniques to process converted-wave data is important.
Much progress has been made in many areas
of converted-wave seismic processing, such as stacking, DMO, migration
and velocity analysis
Alfaraj (1992); Harrison and Stewart (1993); Huub Den Rooijen (1991); Iverson et al. (1989); Tessmer and Behle (1988).
...
Converted-mode angle-domain common-image gathers for migration velocity analysis
(ps.gz 969K) (pdf 1120K) (src 2071K)
Rosales D. A. and Biondi B.
Common-image gathers are very useful for velocity and
petrophysical analysis. Wavefield-extrapolation methods produce
Angle-Domain Common-Image Gathers (ADCIGs). For the conventional PP
case, ADCIGs are a function of the opening angle.
The representation of ADCIGs for PS data (PS-ADCIGs) is more
elaborate than for conventional ADCIGs. In
PS-ADCIGs,
the P-to-S velocity ratio is a major variable in transforming
the subsurface offset to the opening angle, and in transforming
this opening angle to either the P-incidence
or the S-reflection angle.
Numerical studies show that when the
P-to-S velocity ratio and image midpoint information are not
incorporated the
error in computing PS-ADCIGs is enough to introduce
artifacts in the velocity model.
Orthogonal mesh generation for Riemannian wavefield extrapolation (ps.gz 481K) (pdf 666K) (src 5043K)
Shragge J.
This paper presents a general method for generating 2D or 3D orthogonal
coordinate systems. Developed coordinate systems are triplication
free and appropriate for use in Riemannian wavefield extrapolation.
This method exploits properties of potential function solutions
of Laplace's equation. I show that certain specifications of a
potential function's boundary conditions lead to a physical
representation of equipotential surfaces where there are equivalent to
extrapolation steps. Potential function solutions, obtained through
conjugate gradient solvers, are used subsequently in a phase-ray-tracing
procedure that generates geometric rays orthogonal to the
equipotential surfaces. These rays collectively define an orthogonal
coordinate system linked to the underlying Cartesian mesh through definable
one-to-one mappings. The utility of this approach in generating
coordinate systems is tested on a 2D
model of rugged topography from the Canadian Foothills, and on 3D
topography of the San Francisco Bay area.
Wavefield extrapolation in frequency-wavenumber domain for spatially-varying velocity models (ps.gz 65K) (pdf 60K) (src 241K)
Alvarez G. and Artman B.
Mixed domain wavefield extrapolation methods can handle, to a large extent,
spatial velocity variations by performing part of their computation in the
 -
- domain and part of the computation in the
domain and part of the computation in the
 -
- domain. The best-known mixed domain methods are
...
domain. The best-known mixed domain methods are
...
Migration and modeling of seismic data affected by focusing-effect AVO/AVA (ps.gz 146K) (pdf 98K) (src 133K)
Vlad I.
Focusing-effect AVO or AVA is the phenomenon of velocity and/or
absorption lenses creating substantial amplitude variations, but only
small traveltime anomalies Kjartansson (1979). The patterns
thus created can interfere significantly with AVO/AVA caused by
lithological contrasts at the reflector. To render amplitude analysis
feasible, these patterns need to be removed from the image. I will use the acronym ``FEAVO'' to refer to focusing-effect AVO or AVA in general, reserving ``FEAVA'' only for specific references to the angle domain. These terms refers only to amplitudes focusing through heterogeneities smaller than the Fresnel zone, as formalized by Spetzler et al. (2004), and which do not cause energy to be lost by sending it outside the finite spatial extent of the seismic survey (i.e., ``illumination problems''). Focusing can be positive (usual meaning of term) or negative (i.e., in the case of absorption).
Vlad and Biondi (2002), Vlad (2002),
...
Fourier-domain imaging condition for shot-profile migration (ps.gz 582K) (pdf 316K) (src 1398K)
Artman B. and Fomel S.
Cross-correlating up-coming and down-going wavefields inherently
applies a spatial multiplication. This multiplication could be
performed in the wave-number domain as a convolution. However, the
full imaging condition, including subsurface offset, transforms to a
Fourier domain equivalent that is also a
lagged multiplication. This fact allows for the simple analysis
of anti-aliasing criteria. Migrations with synthetic data with flat and
dipping reflectors in a homogeneous medium are produced to evaluate
the Fourier domain algorithm and shots from the Marmousi data set are
shown as examples of its efficacy. Periodic replications in the
image space are introduced when solving the imaging condition in the
Fourier domain which make results unsatisfactory. The cost of
computing the imaging condition in the Fourier domain is much higher
than its space domain equivalent since very few subsurface offsets
need to be imaged if the velocity model is reasonably accurate.
Analysis of the Fourier domain imaging condition leads to the
conclusion that anti-aliasing efforts can be implemented
post-migration.
A self-adaptive algorithm for choosing reference velocities in the presence of lateral velocity variations (ps.gz 1615K) (pdf 372K) (src 10661K)
Wang H. and Shan G.
Seismic wave propagation depicted with the perturbation theory has important and wide-spread uses in reflection seismology. As we know, in perturbation theory, wave propagation needs a reference velocity. The closer the reference velocity is to the true velocity, the more accurate the wave propagation is. However, it is not easy to choose reasonable reference velocities in the presence of severe lateral velocity variations. Assigning a reference velocity value at each spatial point is not computationally feasible, because there is a trade-off between the calculation cost and the number of reference velocities. We show that the accuracy of seismic wave propagation can be more easily improved by choosing a set of reasonable reference velocities rather than by optimizing a one-way wave propagator. Therefore, we introduce a self-adaptive approach to choose a set of reference velocities for an extrapolation layer, in the presence of lateral velocity variations. Through sorting the velocity data an array with increasing values, and by setting a threshold average-velocity ratio or velocity- variance ratio, we can choose a set of reasonable reference velocities for wavefield extrapolation. This method can also be used for image edge detecting. It is flexible and computationally cost-effective.
Unified seismic-wave imaging - from data space to model space (ps.gz 53K) (pdf 109K) (src 40K)
Wang H. and Shan G.
Under operator, matrix and inverse theory, seismic-wave imaging can be considered a unified process-mapping from data space to model space.
The main topics in seismic-wave imaging include (1) seismic-data interpolation, regularization and redatuming, which mainly decrease the imaging noise; (2) seismic-wave illumination analysis, which predicts whether a target reflector can be imaged and evaluates the suitability of an acquisition configuration in the case of rugged topography and severe lateral velocity variations; and (3) seismic-wave migration/inversion imaging algorithms, which give an imaging result with the help of a wave propagator, known a macro-velocity model.
The last and most important thing is to build an accurate macro-velocity model. All of the processes can be considered with the conjugate operator/matrix under least-squares theory. In this article, we review the following topics: (1) expression of data space and model space; (2) affiliation between data space and model space; (3) seismic-data preprocessing; (4) seismic-data illumination; (5) migration imaging and inversion imaging as least-squares inverse problems; (6) amplitude-preserving migration imaging with wavefield extrapolation; (7) migration velocity analysis and inversion and (8) some related topics. We express the imaging process with the operator or matrix theory and give some directions for further research.
Multiples and noise attenuation
Water-bottom and diffracted 2D multiple reflections in data space and image space (ps.gz 840K) (pdf 467K) (src 5304K)
Alvarez G.
Water-bottom multiples from a dipping interface have the same kinematics
in a Common Midpoint (CMP) gather as a primary from a reflector with twice
the dip at twice the perpendicular depth at the CMP location. When migrated with the
velocity of the primaries, these multiples are overmigrated just as
primaries migrated with higher velocity, and their moveout is thus
predictable in image space. Diffracted
multiples, on the other hand, have an
apex-shifted moveout in CMP gathers and a more complicated, also
apex-shifted, residual moveout in image space when migrated
with the velocity of the primaries. I illustrate the moveout of water-bottom
and diffracted multiples in image space with a simple 2D synthetic dataset.
Multiple attenuation: data space vs. image space - A real data example (ps.gz 6241K) (pdf 1413K) (src 14598K)
Rosales D. A. and Guitton A.
Multiples can be attenuated either before or after the imaging process.
Adaptive subtraction can be applied after migration to eliminate the
multiples in the image space.
We build a multiple model based on the sea floor reflection, that is
kinematically correct. We then perform multiple attenuation to
remove the water-bottom multiple in both the image space and
the data space.
Sparse radon transforms with a bound-constrained approach (ps.gz 534K) (pdf 268K) (src 1192K)
Guitton A.
Radon transforms are popular operators for velocity analysis Guitton and Symes (2003); Taner and Koehler (1969),
noise attenuation Foster and Mosher (1992), and data
interpolation Hindriks and Duijndam (1998); Trad et al. (2002). One property
that is often sought in radon domains is sparseness, where the energy
in the model space is well focused for each corresponding event in the data space.
...
Removal of linear events with combined radon transforms (ps.gz 2293K) (pdf 1333K) (src 6155K)
Artman B. and Guitton A.
We explore the classic signal and noise separation problem of removing
linear events from shot-gathers through several
inversion schemes using a combined modeling operator composed of both
hyperbolic and linear radon transforms. Data are inverted
simultaneously for both linear and hyperbolic moveout which provides
two model-space outputs. These are forward modeled seperately to
provide an output data-space devoid of one of the model-space components.
We employ this approach to analyze the removal of direct arrivals and
ground-roll from shot-gathers. Inversion schemes used imnclude: 1)
bound-constrained, 2) Cauchy norm regularization, 3) Huber norm
approximating the l1 norm, and 4) the l2 norm using linear
least-squares. Synthetic tests and four field shot-gathers are used
to demonstrate the approach. Methods 1, 2, and 3 are designed to provide
sparse model-space inversions. In the real data examples,
the least-squares solution is able to better achieve the signal to
noise separation goal despite its model-space being often
less appealing.
Rock Physics
Using knowledge of microstructure to improve estimates and bounds on elastic constants and transport coefficients in heterogeneous media (ps.gz 99K) (pdf 226K) (src 86K)
Berryman J. G.
The most commonly discussed measures of microstructure in composite
materials are the spatial correlation functions, which in a porous
medium measure either the grain-to-grain correlations, or
the pore-to-pore correlations in space. Improved bounds based on this
information such as the Beran-Molyneux bounds for bulk modulus and
the Beran bounds for conductivity are well-known. It is first shown
how to make direct use of bounds and spatial correlation information
to provide estimates that
always lie between these upper and lower bounds for any
microstructure whenever the microgeometry parameters are known.
Then comparisons are made between these estimates, the bounds, and two
new types of estimates. One new estimate for elastic constants makes
use of the Peselnick-Meister bounds (based on Hashin-Shtrikman
methods) for random polycrystals of laminates to generate
self-consistent values that always lie between the bounds.
A second new type of estimate for conductivity assumes that
measurements of formation factors (of which there are at least
two distinct types in porous media, associated respectively with pores
and grains for either electrical and thermal conductivity)
are available, and computes new bounds based on this information.
The paper compares and contrasts these various methods in order
to clarify just what microstructural information - and how accurately
that information - needs to be known in order to be useful for
estimating material constants in random and heterogeneous media.
Geomechanical constants of heterogeneous reservoirs: pore fluid effects on shear modulus (ps.gz 82K) (pdf 194K) (src 77K)
Berryman J. G.
To provide quantitative measures of the importance of
fluid effects on shear waves in the heterogeneous reservoirs,
a model material called a ``random polycrystal of porous laminates''
is introduced. This model
poroelastic material has constituent grains that are layered (or
laminated), and each layer is an isotropic, microhomogeneous porous
medium. All grains are composed of exactly the same porous
constituents, and have the same relative volume fractions. But the order of
lamination is not important because the up-scaling method used to
determine the transversely isotropic (hexagonal) properties of the grains
is Backus averaging, which - for quasi-static or long-wavelength
behavior - depends only on the volume fractions and layer properties.
Grains are then jumbled together totally at random, filling the reservoir,
and producing an overall isotropic poroelastic medium. The
poroelastic behavior of this medium is then analyzed using the
Peselnick-Meister-Watt bounds (of Hashin-Shtrikman type). We study
the dependence of the shear modulus on pore fluid
properties and determine the expected range of behavior. In
particular we compare and contrast these results with those anticipated
from Gassmann's fluid substitution formulas, and to the predictions of
Mavko and Jizba for very low porosity rocks with flat cracks.
This approach also permits
the study of arbitrary numbers of constituents, but for simplicity the
numerical examples are restricted here to just two constituents. This
restriction also permits the use of some special exact results
available for computing the overall effective stress coefficient
in any two-component porous medium.
The bounds making use of polycrystalline microstructure are very tight.
Results for shear modulus demonstrate that the ratio of compliance
differences R
(i.e., shear compliance changes over bulk compliance changes)
is usually nonzero and can take a wide range of values, both above and
below the value R = 4/15 for low porosity, very low aspect ratio
flat cracks. Results show the overall shear modulus in this model
can depend relatively strongly on mechanical properties of the pore
fluids, sometimes (but rarely) more strongly than the dependence of the
overall bulk modulus on the fluids.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
6/6/2005
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)