

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
SEP-129 -- TABLE OF CONTENTS
Imaging
3D plane-wave migration in tilted coordinates (ps.gz 2871K) (pdf 586K) (src 4787K)
Shan G., Clapp R., and Biondi B.
We develop 3D plane-wave migration in tilted coordinates for anisotropic media.
We transform the recorded surface data to plane-wave data by slant-stack processing.
Both the source plane-wave and its corresponding slant-stacked data
are extrapolated into the subsurface within a tilted coordinates system whose direction depends on
the propagation direction of the plane-wave. Images are generated by cross-correlating these two
wavefields. A real dataset from Gulf of Mexico shows that this technique
can image steeply dipping salt flanks and faults, even though the one-way wave equation operator is
used for the wavefield extrapolation.
Prestack depth migration in elliptic coordinates (ps.gz 12758K) (pdf 1857K) (src 64345K)
Shragge J. and Shan G.
We extend Riemannian wavefield extrapolation (RWE) to prestack
migration using 2D elliptic coordinate systems. The
corresponding 2D elliptic extrapolation wavenumber introduces only a
slowness model stretch to the
single-square-root operator, enabling the use of existing Cartesian
implicit finite-difference extrapolators for propagating wavefields. A
zero-offset migration example illustrates the advantages of elliptic
coordinates in imaging overturning wavefields. Imaging tests of
the SMAART JV Pluto 1.5 and BP velocity benchmark data sets illustrate that
the RWE migration algorithm generates high-quality prestack
migration images equal to, or better than, the corresponding
Cartesian coordinate systems. We still require higher-order
extrapolators for accurate propagation and imaging using one-way
wave equations, even in situations where RWE geometries are
employed.
A tutorial on optimizing time domain finite-difference schemes: "Beyond Holberg" (ps.gz 49K) (pdf 114K) (src 4771K)
Etgen J. T.
Time-domain finite-difference solutions to the wave equation are a standard method
for modeling seismic wave propagation, but they see limited use in data processing because they
are expensive to compute. Given the resurgence of interest in reverse-time migration,
anything that improves the performance and accuracy of the finite-difference method may be worthwhile.
Additionally, the design problem for optimal finite-difference operators is a "simple and approachable"
problem for teaching non-linear least squares.
The standard solution for improving the finite-difference method is to use long spatial difference
operators. However, there are computational reasons why it might be preferable to use spatially compact stencils, assuming
they can be made accurate enough.
Two-way vs. one-way: (ps.gz 1622K) (pdf 815K) (src 7258K)
Valenciano A. A.
The one-way wave-equation approximation has a big impact on migration, modeling, and wave-equation inversion. That is why Amplitude vs. subsurface-offset (AVO), and amplitude vs. reflection angle (AVA) responses of the migration of a two-way and a one-way modeled datasets show different illumination patterns.
Deconvolution by the one-way wave-equation Hessian can be use to
account for the illumination problem. But the approximations used to
compute the Hessian have an impact on how effectively the medium AVO and AVA is recover by the inversion.
Optimized implicit finite-difference migration for TTI media: A 2D synthetic dataset (ps.gz 193K) (pdf 185K) (src 2556K)
Shan G.
I review optimized implicit finite-difference migration for tilted TI media. The
implicit finite-difference scheme is designed by fitting the dispersion relation with rational functions
using least-squares optimization. I apply the method to a synthetic dataset. The result shows that
the algorithm can handle laterally varying tilted TI media.
Inversion
Target-oriented wave-equation inversion: Sigsbee model (ps.gz 421K) (pdf 253K) (src 11092K)
Valenciano A. A.
A complex velocity model can cause shadow zones in an image computed by migration due to poor illumination. These shadow zones may contain weak signals masked by artifacts. To reduce artifacts and recover the real signal, a target-oriented wave-equation inversion scheme can be developed that uses an explicitly computed least squares inversion Hessian. To solve the otherwise ill-conditioned inversion problem a model regularization needs to be added. One choice for regularization is to use the customary damping in the image space, another is to penalize the energy in the image not focused at zero subsurface-offset. To apply the second, the subsurface-offset Hessian needs to be computed by using the adjoint of migration as the modeling operator. Results on Sigsbee model show encouraging results.
Non-stationary interpolation in the f-x domain (ps.gz 1880K) (pdf 1099K) (src 6923K)
Curry W.
Interpolation of seismic data has previously been performed using
non-stationary prediction-error filters in the t-x domain. This
methodology is applied in the f-x domain,
and is tested on synthetic data as well as 3D pre-stack marine data in various
domains. Benefits include a reduced memory footprint and computational cost,
which leads to the ability to interpolate in higher dimensions than with t-x
domain interpolation. However, one severe drawback is the assumption of stationarity in
time.
Interpolation with pseudo-primaries: revisited (ps.gz 3065K) (pdf 1192K) (src 13027K)
Curry W.
Large gaps may exist in marine data at near offsets. I generate pseudo-primaries
by auto-correlating data containing both primary and multiple reflections.
These pseudo-primaries are used as training data for a non-stationary prediction-error
filter, which is then used to interpolate the missing near offsets. This
method yields good results using filters in the t-x domain, whereas f-x
domain filters do not fare well at eliminating the crosstalk in the pseudo-primaries.
Seismic monitoring of sub-salt reservoirs: Time-lapse wave-equation inversion (ps.gz 277K) (pdf 402K) (src 4309K)
Ayeni G. and Biondi B.
Time-lapse seismic is now a core technology for reservoir monitoring
and characterization. However, many challenges continue
to exist in its application in complex geology (e.g. sub-salt
reservoirs). Differences in acquisition geometry (non-repeatability)
and poor illumination are examples of factors that cause contamination
of the desired time-lapse effects (i.e. changes due to production).
By computing the time-lapse response as a difference between
least-squares inverse images or posing time-lapse imaging as a
least-squares
inverse problem, we hope to attenuate geometry and other unwanted effects.
Velocity
Transmission wavefield velocity analysis (ps.gz 41K) (pdf 100K) (src 20K)
Shragge J.
Transmission wavefields contain important information on
subsurface velocity profiles. This is evident from the many
tomography-based techniques that invert for perturbations on an
assumed background velocity using the transmission wavefield response.
One of the more successful approaches is waveform tomography
Pratt and Worthington (1989); Woodward (1992), an approach to non-linear velocity inversion problem that
iteratively obtains an estimate of velocity perturbations by minimizing
the difference between forward-modeled waveforms and acquired data
...
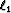 Regularized Inversion (ps.gz 209K) (pdf 235K) (src 28291K)
Regularized Inversion (ps.gz 209K) (pdf 235K) (src 28291K)
Witten B.
Here an interior point inversion
method is presented that solve a least squares problem with 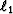 regularization.
Velocity inversion can benefit from
regularization.
Velocity inversion can benefit from 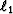 regularization
because the sparse solution creates blocky velocity models. This is
often more geologically accurate than smooth models. In this paper
an efficient method is present for solving
regularization
because the sparse solution creates blocky velocity models. This is
often more geologically accurate than smooth models. In this paper
an efficient method is present for solving 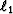 regularized least
squares problems. Its usefulness is shown through comparisons of
previous methods on an example using a least squares formulation for
Dix inversion.
regularized least
squares problems. Its usefulness is shown through comparisons of
previous methods on an example using a least squares formulation for
Dix inversion.
Full-volume dip corrections for velocity analysis and MVA (ps.gz 1952K) (pdf 591K) (src 5197K)
GR.
Picking of stacking velocities and residual migration velocities can be difficult in noisy data. Common solutions involve the creation of super-gathers, stacking semblance panels, and flattening data along picked horizons. This report shows that full-volume dip corrections can be used for practical enhancements to velocity analysis workflows. The dip fields are computed both with a semblance method and plane-wave deconstruction filters. Following equations from common reflection surface (CRS) processing, the dip fields are used to extend the standard move-out equations to more precisely describe reflections in super-gathers. This correction improves the sharpness of semblance panels and makes it possible to use larger panels than would be possible without the corrections. The report shows 3D examples of using the full-volume dip information both for conventional stacking and pre-stack time migration.
Aligned vertical fractures, (ps.gz 42K) (pdf 260K) (src 30K)
Berryman J. G.
The Sayers and Kachanov (1991) crack-influence parameters are
shown to be directly related to Thomsen (1986) weak-anisotropy seismic
parameters for fractured reservoirs when the crack/fracture density
is small enough. These results are then applied to the
problem of seismic wave propagation in reservoirs having HTI symmetry
due to the presence of aligned vertical fractures. The approach suggests
a method of inverting for fracture density from wave speed data.
Gathers
Moveout analysis with flattening (ps.gz 1066K) (pdf 392K) (src 2143K)
Clapp R. G.
Moveout analysis is an important component of many
data processing steps. The most basic application
is Normal Moveout (NMO), where curvature is
related to velocity. Radon based multiple removal
techniques take advantage of the differing moveout
of primaries and multiples Hampson (1986). Migration velocity
analysis often measures curvature in common reflection point
gathers in either the offset domain or angle domain.
...
Selective stacking in the reflection-angle and azimuth domain (ps.gz 2459K) (pdf 5090K) (src 5631K)
Tang Y.
I analytically demonstrate the existence of artifacts in angle-domain common-image gathers (ADCIGs)
caused by sparsely sampled wavefields from the perspective of shot-profile migration.
The subsurface-offset domain common-image gather (SODCIG) is linearly related to the ADCIG in
locally constant-velocity media when the wavefields are sufficiently well sampled,
but not when the wavefields are poorly sampled. Hence, linear slant-stack or radial-trace transform
in SODCIGs will produce ADCIGs with artifacts, which might hinder further interpretation or analysis and
reduce the quality of the final stacking image. Instead of simply stacking along reflection angle and azimuth axes,
I present a method to compute the stacking weights as functions of angle and azimuth and make the stacking process selective. My method
is tested on the synthetic wide-azimuth version of the SEG/EAGE salt data set, where a cleaner image with higher signal-to-noise ratio is obtained.
Anisotropic migration velocity analysis from residual moveout transformation in angle-domain common-image gathers (ps.gz 3504K) (pdf 1076K) (src 33706K)
Jousselin P. and Biondi B.
We present the application of anisotropic migration velocity
analysis (MVA) on synthetic data and on a real dataset acquired in the
North Sea. The method we use to estimate anisotropic migration velocities is
based on the computation and analysis of angle-domain common-image
gathers (ADCIGs) in conjunction with anisotropic
wavefield-continuation migration. Assuming flat
reflectors and vertically transversely isotropic (VTI) media, we compute
anisotropic velocity spectra from a residual moveout (RMO)
transformation, based on the theoretical expression of the RMO in anisotropic
ADCIGs as a function of perturbations in migration velocities.
In the first part of this paper, we briefly present the theory of
ADCIGs and the derivation of the mathematical expression of the RMO
function. In the second part, we analyze synthetic data with the method
we propose to estimate anisotropic migration velocities. We
demonstrate that our method is unable to resolve vertical
velocities but nevertheless accurately estimates horizontal and normal moveout
(NMO) velocities even for significant perturbations in the velocity
model, provided the range of aperture angle is not too small. In the
last part of this paper, we demonstrate on real data the validity of
our estimation method, by showing it indicates the presence of
velocity anellipticity in layers stratigraphically interpreted as anisotropic
and for which well data do not match seismic data migrated under the assumption
of isotropy.
Mapping of 3-D multiples to image space: An example with a Gulf of Mexico dataset (ps.gz 5057K) (pdf 1349K) (src 28877K)
Alvarez G.
I migrate a real 3D seismic dataset from the Gulf of Mexico with
shot profile migration and use it to illustrate the mapping of 3D multiples
from data space to image space. The dataset contains specular water-bottom multiples,
peg-leg multiples associated with a large, shallow salt body, and
diffracted multiples originating at the salt edges. Both the water
bottom and the salt body have significant cross-line dip which makes it
difficult to model the trajectory of the multiples. The location of the
multiples in the image domain is severely affected by the presence of the
salt and thus do not follow the geometry of the multiple-generating
interface. As a consequence, some multiples could easily be interpreted as
primaries. I show, by computing subsurface offsets for one sail-line,
that the multiples map away from the zero-subsurface offset as they would
in a purely 2D model.
Improving multiple prediction in image space using ADCIGs for limited-offset recordings (ps.gz 5340K) (pdf 1240K) (src 10750K)
Vyas M.
Auto-convolution is a convenient way of generating multiple models and is the basis for Surface Related Multiple Prediction (SRMP). The completeness of the multiple model, however, relies on recording all the primary paths that contribute to multiple generation. In practice, with limited offset recordings and in areas of complex subsurface geometries (especially steep dips), we might record only the multiple path and not the primary, leading to incomplete multiple models. In image space, this translates to modeling multiples at fewer opening angles than are actually present. In this article, I show that the Angle Domain Common Image Gathers (ADCIGs) of multiple models provide useful angular information which may be used to infill or extrapolate missing angles and account for the missing multiples in the model generated using SRMP.
Residual multiple attenuation using AVA modeling (ps.gz 4251K) (pdf 1076K) (src 11681K)
Guerra C.
Residual multiple attenuation is a common process applied towards the end of the seismic processing flow.
Its main objective is to decrease the energy of migrated residual multiples. This process can be time-consuming.
I present a method which uses amplitude-versus-angle (AVA) modeling to simulate primary events and adaptive subtraction to estimate residual multiples and residual-multiple-attenuated data. The method is applied
on angle-domain common-image gathers (ADCIGs) from a 2D data set from the Gulf of Mexico that is contaminated with residual multiples. This method is simple, fast and, depending on the
parameterization of the adaptive subtraction, can preserve primary reflection amplitudes.
Computers
A New Build Environment for SEP (ps.gz 13K) (pdf 53K) (src 5K)
Witten B., Curry B., and Shragge J.
The Stanford Exploration Project (SEP) has been at the forefront of
computational reproducible research for many years. Beginning with
the introduction of active (a-doc) and interactive
(i-doc) documents by Claerbout (1990), SEP progressed to reproducible
scripting using cake Nichols and Cole (1989) and archiving
on CD-ROMS to ensure that entire reports, along with original codes
and processing flows, could be distributed easily and cheaply. An
additional change occurred around SEP-89 when the more flexible GNU
...
Accelerating subsurface offset gathers for (ps.gz 383K) (pdf 195K) (src 639K)
Pell O. and Clapp R. G.
For shot profile migration construction of subsurface offset
gathers can be the dominant cost. By implementing the subsurface offset gather computation on a MAX-1
accelerator card with a Xilinx Virtex-4 Field Programable
Gate Array (FPGA), we obtain 20x speed-up over a state-of-the-art
Opteron system. By reducing data precision further speed-up can be achieved,
at minimal image degradagation.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
6/19/2007
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)