




Next: Waveform Inversion in Riemannian
Up: Shragge: TWVA
Previous: Conclusion
- Operto, S., J. Virieux, et al., 2006, 3D frequency-domain finite-difference modeling of acoustic waves using a massively parallel direct solver: A feasibility study: 75th SEG Ann. Gen. Meeting Conference and Exhibition, Expanded Abstracts.
-
- Pratt, R. and M. Worthington, 1989, The application of diffraction tomography to cross-hole seismic data: Geophysics, 53, 1284-1294.
-
- Sava, P. and B. Biondi, 2004, Wave-equation migration velocity analysis. I. Theory: Geophysical Prospecting, 52, 593-606.
-
- Sava, P. and S. Fomel, 2005, Riemannian wavefield extrapolation: Geophysics, 70, T45-T56.
-
- Shragge, J., 2006, Non-orthogonal Riemannian wavefield extrapolation: 75th SEG Ann. Gen. Meeting and Exhibition, Expanded Abstracts, 2236-2240.
-
- Sirgue, L. and R. Pratt, 2004, Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies: Geophysics, 69, 231-248.
-
- Stekl, I. and R. Pratt, 1998, Accurate visco-elastic modeling frequency-domain finite differences using rotated operators: Geophysics, 63, 1779-1794.
-
- Woodward, M., 1992, Wave-equation tomography: Geophysics, 57, 15-26.
-
APPENDIX A
This appendix develops a WEMVA scattering operator Sava and Biondi (2004)
for use in transmission wavefield waveform inversion. The
extrapolation operator, 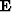 , is given by,
, is given by,
| ![\begin{displaymath}
{\mathbf E}_z[] = {\rm e}^{{\rm i} k_z \Delta z},\end{displaymath}](img64.gif) |
(29) |
where kz is the depth wavenumber and 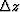 is the
extrapolation depth step. The extrapolation wavenumber in depth is
given by
is the
extrapolation depth step. The extrapolation wavenumber in depth is
given by
| 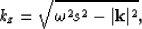 |
(30) |
where 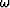 is temporal frequency and
is temporal frequency and 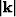 is the horizontal
wavenumber magnitude.
is the horizontal
wavenumber magnitude.
The vertical wavenumber can be separated into two components, one
corresponding to the background medium, 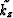 , and one
corresponding to a perturbation,
, and one
corresponding to a perturbation, 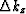 , such that,
, such that,
| 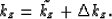 |
(31) |
In a first-order approximation, we can relate these two extrapolation
wavenumbers by a Taylor-series expansion,
| 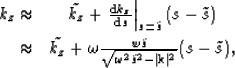 |
|
| (32) |
where s(x,z) is the slowness and 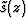 corresponds to a
background slowness.
corresponds to a
background slowness.
Within any depth slab we can extrapolate the wavefield from the top,
either in the perturbed or in the background medium. The wavefields
at the bottom of the slab, 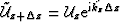 and
and 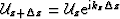 , related by,
, related by,
| 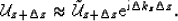 |
(33) |
Equation 34 is a direct statement of the Rytov
approximation, because the wavefields at the bottom of the slab
correspond to different phase shifts related by a linear equation.
Thus, we obtain the wavefield perturbation 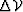 at the bottom of the
slab by subtracting the background wavefield
at the bottom of the
slab by subtracting the background wavefield 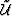 from the
perturbed wavefield
from the
perturbed wavefield 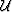 :
:
| 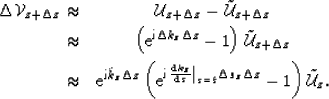 |
|
| (34) |
| |
For the Born approximation, we further assume that the wavefield
differences are small so that we linearize the exponential
function according to 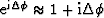 . With this approximation we write the
following downward continued scattered wavefield,
. With this approximation we write the
following downward continued scattered wavefield,
| 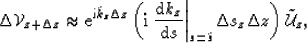 |
(35) |
which, in operator form is
| ![\begin{displaymath}
\S_z(\tilde{{\mathcal U}}_z [\Delta s_z]) \approx {\rm i} \l...
...vert _{s=\tilde{s}} \Delta s_z \Delta z \tilde{{\mathcal U}}_z.\end{displaymath}](img80.gif) |
(36) |
The Born operator may be implemented in the Fourier domain relative to
a constant reference slowness in any individual slab. In this case,
| 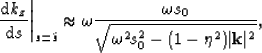 |
(37) |
where  is a damping parameter to avoid division by zero.
is a damping parameter to avoid division by zero.
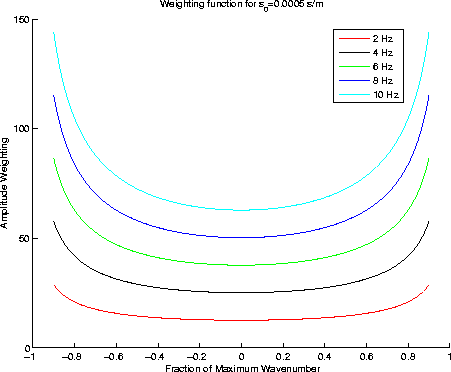
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the amplitude weighting demanded by
the filter in equation 38 for five different
frequencies for slowness 0.5 s/km.
shows the amplitude weighting demanded by
the filter in equation 38 for five different
frequencies for slowness 0.5 s/km.
KXfilter
Figure 1 Example of the Born amplitude weighting
function demanded by the WEMVA theory for a slowness of 0.5 s/km
and a damping factor of 0.001.
|
|  |

![]() , and one
corresponding to a perturbation,
, and one
corresponding to a perturbation, ![]() , such that,
, such that,
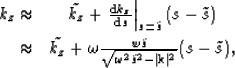
![]() and
and ![]() , related by,
, related by,
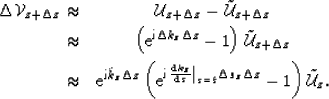
![]() . With this approximation we write the
following downward continued scattered wavefield,
. With this approximation we write the
following downward continued scattered wavefield,
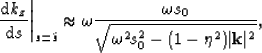
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the amplitude weighting demanded by
the filter in equation 38 for five different
frequencies for slowness 0.5 s/km.
shows the amplitude weighting demanded by
the filter in equation 38 for five different
frequencies for slowness 0.5 s/km.
