

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
SEP-SERGEY -- TABLE OF CONTENTS
Optimization
Searching the Sea of Galilee: The splendors and miseries of iteratively reweighted least squares (ps.gz 818K) (pdf 860K) (src 46K)
Fomel S. and Claerbout J. F.
We applied the inverse linear interpolation method to process a
bottom sounding survey data set from the Sea of Galilee in Israel.
Non-Gaussian behavior of the noise led us to employ a version of the
iteratively reweighted least squares (IRLS) technique. The IRLS enhancement
of the method was able to remove the image artifacts caused by the
noise at the cost of a loss in the image resolution. Untested
alternatives leave room for further research.
Least-square inversion with inexact adjoints. Method of conjugate directions: A tutorial (ps.gz 300K) (pdf 331K) (src 43K)
Fomel S.
This tutorial describes the classic method of conjugate directions:
the generalization of the conjugate-gradient method in iterative
least-square inversion. I derive the algebraic equations of the
conjugate-direction method from general optimization
principles. The derivation explains the ``magic'' properties of
conjugate gradients. It also justifies the use of conjugate
directions in cases when these properties are distorted
either by computational errors or by inexact adjoint operators. The
extra cost comes from storing a larger number of previous search directions
in the computer memory. A simple ratfor program and three examples
illustrate the method.
Stacking operators: Adjoint versus asymptotic inverse (ps.gz 340K) (pdf 423K) (src 29K)
Fomel S.
The paper addresses the theory of stacking operators used in
seismic data processing. I compare the notion of asymptotically
inverse operators with the notion of adjoint operators. These two
classes of operators share the same kinematic properties, but their
amplitudes (weighting functions) are defined differently. I introduce
the notion of the asymptotic pseudo-unitary operator, which possesses
both the property of being adjoint and the property of being
asymptotically inverse. The weighting function of the asymptotic
pseudo-unitary stacking operator is completely defined by its
kinematics. I exemplify the general theory by considering such
stacking operators as Kirchhoff datuming, migration, offset
continuation, DMO, and velocity transform.
Iterative methods of optimization with application to crosswell tomography (ps.gz 49K) (pdf 80K) (src 54K)
Berryman J. G. and Fomel S.
We review the theory of iterative optimization, revealing the common
origin of different optimization methods and reformulating the
pseudoinverse, model resolution, and data resolution operators in
terms of effective iterative estimates. Examples from crosswell
tomography illustrate the theory and suggest efficient methods of its
implementation.
On model-space and data-space regularization: (ps.gz 848K) (pdf 1015K) (src 44K)
Fomel S.
Constraining ill-posed inverse problems often requires
regularized optimization. I describe two alternative approaches to
regularization. The first approach involves a column operator and an
extension of the data space. The second approach constructs a row
operator and expands the model space. In large-scale problems, when
the optimization is incomplete, the two methods of regularization
behave differently. I illustrate this fact with simple examples and
discuss its implications for geophysical problems.
On the general theory of data interpolation (ps.gz 62K) (pdf 108K) (src 21K)
Fomel S.
Data interpolation is one of the most important tasks in
geophysical data processing. Its importance is increasing with the
development of 3-D seismics, since most of the modern 3-D
acquisition geometries carry non-uniform spatial distribution of
seismic records. Without a careful interpolation, acquisition
irregularities may lead to unwanted artifacts at the imaging step
Chemingui and Biondi (1996); Gardner and Canning (1994).
...
Spitz makes a better assumption for the signal PEF (ps.gz 49K) (pdf 72K) (src 14K)
Claerbout J. and Fomel S.
In real-world extraction of signal from data
we are not given the needed signal prediction-error filter (PEF).
Claerbout has taken S, the PEF of the signal,
to be that of the data, 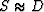 . Spitz takes it to be
. Spitz takes it to be 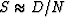 . Where noises are highly predictable in time or space,
Spitz gets significantly better results.
Theoretically, a reason is that the essential character
of a PEF is contained where it is small.
. Where noises are highly predictable in time or space,
Spitz gets significantly better results.
Theoretically, a reason is that the essential character
of a PEF is contained where it is small.
Seismic data interpolation with the offset continuation equation (ps.gz 1343K) (pdf 1246K) (src 30K)
Fomel S.
I propose a finite-difference offset continuation filter for
interpolating seismic reflection data. The filter is constructed
from the offset continuation differential equation and is applied on
frequency slices in the log-stretch frequency domain. Synthetic data
tests produce encouraging results: nearly perfect interpolation of a
constant-velocity dataset with a complex reflector model and
reasonably good interpolation of the Marmousi dataset.
Speculations on contouring sparse data: Gaussian curvature (ps.gz 29K) (pdf 40K) (src 11K)
Claerbout J. and Fomel S.
We speculate about regularizing (interpolating) sparse data.
We speculate that L1 regularization would be desirable.
An example convinces us it would not.
Changing direction we learn that
flexed paper has zero Gaussian curvature.
Unfortunately, Gaussian curvature
is a nonlinear function of the altitude.
Applications of plane-wave destructor filters (ps.gz 1758K) (pdf 1606K) (src 67K)
Fomel S.
On several synthetic and real-data examples, I show that
finite-difference plane-wave destructor filters can be a valuable
alternative to prediction-error filters in applications such as data
interpolation, fault detection, and noise attenuation.
Inverse B-spline interpolation (ps.gz 1783K) (pdf 1779K) (src 38K)
Fomel S.
B-splines provide an accurate and efficient method for
interpolating regularly spaced data. In this paper, I study the
applicability of B-spline interpolation in the context of the
inverse interpolation method for regularizing irregular data.
Numerical tests show that, in comparison with lower-order linear
interpolation, B-splines lead to a faster iterative conversion in
under-determined problems and a more accurate result in
over-determined problems. In addition, they provide a constructive
method for creating discrete regularization operators from continuous
differential equations.
Test case for PEF estimation with sparse data II (ps.gz 44K) (pdf 82K) (src 8K)
Brown M., Claerbout J., and Fomel S.
The two-stage missing data interpolation approach of Claerbout (1999) (henceforth, the GEE
approach) has been applied
with great success Clapp et al. (1998); Crawley (2000); Fomel et al. (1997) in the past.
The main strength of the approach lies in the ability of the prediction error filter (PEF) to
find multiple, hidden correlation in the known data, and then, via regularization, to impose
...
Helix Transform
Missing data interpolation by recursive filter preconditioning (ps.gz 277K) (pdf 277K) (src 65K)
Fomel S., Clapp R., and Claerbout J.
Missing data interpolation problems can be conveniently
preconditioned by recursive inverse filtering. A helix transform
allows us to implement this idea in the multidimensional case. We
show with examples that helix preconditioning can give a
magnitude-order speedup in comparison with the older methods.
Solution steering with space-variant filters (ps.gz 677K) (pdf 645K) (src 103K)
Clapp R. G., Fomel S., and Claerbout J.
Most geophysical problem require some type of regularization.
Unfortunately most regularization schemes produce ``smeared'' results
that are often undesirable when applying other criteria (such as geologic
feasibility).
By forming regularization operators in terms of
recursive steering filters, built from a priori information sources,
we can efficiently guide the solution towards
a more appealing form. The steering
methodology proves effective in interpolating
low frequency functions, such as velocity,
but performs poorly when encountering multiple
dips and high frequency data. Preliminary results using steering filters for
regularization in tomography problems are encouraging.
Exploring three-dimensional implicit wavefield extrapolation with the helix transform (ps.gz 474K) (pdf 440K) (src 43K)
Fomel S. and Claerbout J. F.
Implicit extrapolation is an efficient and unconditionally
stable method of wavefield continuation. Unfortunately, implicit
wave extrapolation in three dimensions requires an expensive
solution of a large system of linear equations. However, by mapping
the computational domain into one dimension via the helix transform,
we show that the matrix inversion problem can be recast in terms of
an efficient recursive filtering. Apart from the boundary
conditions, the solution is exact in the case of constant
coefficients (that is, a laterally homogeneous velocity.) We
illustrate this fact with an example of three-dimensional velocity
continuation and discuss possible ways of attacking the problem of
lateral variations.
Wilson-Burg spectral factorization with application to helix filtering (ps.gz 30K) (pdf 42K) (src 12K)
Sava P., Rickett J., Fomel S., and Claerbout J.
Spectral factorization methods are used for the estimation of
minimum - phase time series from a given power spectrum.
We present an efficient technique for spectral factorization, based
on Newton's method. We show how to apply the method to the
factorization of both auto and cross-spectra, and present a simple
example of 2-D deconvolution in the helical coordinate system.
Directional smoothing of non-stationary filters (ps.gz 404K) (pdf 481K) (src 63K)
Clapp R. G., Fomel S., Crawley S., and Claerbout J. F.
Space-varying prediction error filters are an effective tool in solving
a number of common geophysical problems. To estimate these
filters some type of regularization is necessary. An effective method
is to smooth the filters along radial lines in CMP gathers
where dip information
is relatively unchanging.
Spectral factorization revisited (ps.gz 40K) (pdf 111K) (src 6K)
Sava P. and Fomel S.
In this paper, we review some of the iterative methods for the square
root, showing that all these methods belong to the same
family, for which we find a general formula. We then explain how those
iterative methods for real numbers can be extended to spectral
factorization of auto-correlations. The iteration based on
the Newton-Raphson method is optimal from the convergence stand point, though
it is not optimal as far as stability is concerned. Finally, we show
that other members of the iteration family are more stable, though
slightly more expensive and slower to converge.
Plane wave prediction in 3-D (ps.gz 549K) (pdf 427K) (src 22K)
Fomel S.
The theory of plane-wave prediction in three dimensions is described
by Claerbout (1993, 1997). Predicting a
local plane wave with T-X filters amounts to finding a pair of
two-dimensional filters for two orthogonal planes in the 3-D space.
Each of the filters predicts locally straight lines in the
corresponding plane. The system of two 2-D filters is sufficient for
predicting all but purely vertical plane waves, in which case a third
...
Helical preconditioning and splines in tension (ps.gz 1378K) (pdf 1253K) (src 13K)
Fomel S.
Splines in tension are smooth interpolation surfaces whose
behavior in unconstrained regions is controlled by the tension
parameter. I show that such surfaces can be efficiently constructed
with recursive filter preconditioning and introduce a family of
corresponding two-dimensional minimum-phase filters. The filters are
created by spectral factorization on a helix.
Imaging
The time and space formulation of azimuth moveout (ps.gz 269K) (pdf 786K) (src 20K)
Fomel S. and Biondi B. L.
Azimuth moveout (AMO) transforms 3-D prestack seismic data from one
common azimuth and offset to different azimuths and offsets.
AMO in the time-space domain is represented by a three-dimensional
integral operator. The operator components are the summation path,
the weighting function, and the aperture. To determine the summation path and
the weighting function, we derive the AMO operator by cascading dip
moveout (DMO) and inverse DMO for different azimuths in the time-space
domain. To evaluate the aperture, we apply a geometric approach,
defining AMO as the result of cascading prestack migration (inversion)
and modeling. The aperture limitations provide a consistent
description of AMO for small azimuth rotations (including zero) and justify the
economic efficiency of the method.
Evaluating the Stolt stretch parameter (ps.gz 72K) (pdf 112K) (src 37K)
Fomel S.
The Stolt migration extension to a varying velocity case (Stolt
stretch) implies
describing a vertical heterogeneity by a constant parameter
(W). This paper
exploits the connection between modified dispersion relations and traveltime
approximations to derive an
explicit expression for W. The expression provides theoretically the
highest possible accuracy
within
the Stolt
stretch framework. Applications considered include optimal partitioning
of the velocity distribution for the cascaded migrations and extension
of the Stolt stretch method to transversally isotropic models.
Traveltime computation with the linearized eikonal equation (ps.gz 60K) (pdf 97K) (src 14K)
Fomel S.
Traveltime computation is an important part of seismic imaging
algorithms. Conventional implementations of Kirchhoff migration
require precomputing traveltime tables or include traveltime
calculation in the innermost computational loop . The cost of
traveltime computations is especially noticeable in the case of 3-D
prestack imaging where the input data size increases the level of
nesting in computational loops.
The eikonal differential equation is the basic mathematical model,
...
Implicit 3-D depth migration by wavefield extrapolation with helical boundary conditions (ps.gz 175K) (pdf 179K) (src 31K)
Rickett J., Claerbout J., and Fomel S.
Wavefield extrapolation in the 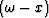 domain provides a tool for
depth migration with strong lateral variations in velocity.
Implicit formulations of depth extrapolation have several advantages
over explicit methods.
However, the simple 3-D extension of conventional 2-D wavefield
extrapolation by implicit finite-differencing requires the
inversion of a 2-D convolution matrix which is computationally
difficult.
In this paper, we solve the 45 wave equation
with helical boundary conditions on one of the spatial axes.
These boundary conditions reduce the 2-D convolution
into an equivalent 1-D filter operation. We then factor this 1-D
filter into causal and anti-causal parts using an extension of
Kolmogoroff's spectral factorization method, and invert the
convolution operator efficiently by 1-D recursive filtering.
We include lateral variations
in velocity by factoring spatially variable filters, and
non-stationary deconvolution.
The helical boundary conditions allow the 2-D convolution matrix to be
inverted directly without the need for splitting approximations, with
a cost that scales linearly with the size of the model space. Using
this methodology, a whole range of implicit depth migrations may now be
feasible in 3-D.
domain provides a tool for
depth migration with strong lateral variations in velocity.
Implicit formulations of depth extrapolation have several advantages
over explicit methods.
However, the simple 3-D extension of conventional 2-D wavefield
extrapolation by implicit finite-differencing requires the
inversion of a 2-D convolution matrix which is computationally
difficult.
In this paper, we solve the 45 wave equation
with helical boundary conditions on one of the spatial axes.
These boundary conditions reduce the 2-D convolution
into an equivalent 1-D filter operation. We then factor this 1-D
filter into causal and anti-causal parts using an extension of
Kolmogoroff's spectral factorization method, and invert the
convolution operator efficiently by 1-D recursive filtering.
We include lateral variations
in velocity by factoring spatially variable filters, and
non-stationary deconvolution.
The helical boundary conditions allow the 2-D convolution matrix to be
inverted directly without the need for splitting approximations, with
a cost that scales linearly with the size of the model space. Using
this methodology, a whole range of implicit depth migrations may now be
feasible in 3-D.
Angle-gather time migration (ps.gz 1241K) (pdf 1198K) (src 14K)
Fomel S. and Prucha M.
Angle-gather migration creates seismic images for different
reflection angles at the reflector. We formulate an angle-gather
time migration algorithm and study its properties. The algorithm
serves as an educational introduction to the angle gather concept.
It also looks attractive as a practical alternative to conventional
common-offset time migration both for velocity analysis and for
AVO/AVA analysis.
Iterative resolution estimation in Kirchhoff imaging (ps.gz 1690K) (pdf 1553K) (src 50K)
Clapp R. G., Fomel S., and Prucha M.
We apply iterative resolution estimation to least-squares
Kirchhoff migration. Resolution plots reveal low illumination areas
on seismic images and provide information about image
uncertainties.
On Stolt stretch time migration (ps.gz 3929K) (pdf 3468K) (src 26K)
Vaillant L. and Fomel S.
We implement Stolt-stretch time migration with an analytical
formulation for the optimal stretch parameter and show how it improves
the quality of imaging.
By a cascaded f-k migration approach with this
algorithm, we manage to obtain time migration results on real data
comparable to Gazdag's
phase-shift method, with a high accuracy for steeply deeping events at
a computational cost dramatically lowered.
Angle-gathers by Fourier Transform (ps.gz 1389K) (pdf 1236K) (src 277K)
Sava P. and Fomel S.
In this paper, we present a method for computing angle-domain
common-image gathers from wave-equation depth-migrated seismic
images. We show that the method amounts to a radial-trace transform
in the Fourier domain and that it is equivalent to a slant stack in
the space domain. We obtain the angle-gathers using a stretch
technique that enables us to impose smoothness through
regularization. Several examples show that our method is accurate,
fast, robust, easy to implement and that it can be used for real
3-D prestack data in applications related to velocity analysis and
amplitude-versus angle (AVA) analysis.
Traveltimes
``Focusing'' eikonal equation and global tomography (ps.gz 561K) (pdf 816K) (src 12K)
Biondi B., Fomel S., and Alkhalifah T.
The transformation of the eikonal equation from depth
coordinates (z,x)
into vertical-traveltime coordinates (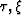 )enables the computation of reflections traveltimes
independent of depth-mapping.
This separation allows
the focusing and mapping
steps to be performed sequentially
even in the presence of complex velocity functions,
that otherwise would ``require'' depth migration.
The traveltimes satisfying the transformed eikonal equation
can be numerically evaluated by solving the associated
ray tracing equations.
The application of Fermat's principle
leads to the expression of linear relationships
between perturbations in traveltimes and
perturbations in focusing velocity.
This linearization, in conjunction with ray tracing,
can be used for a tomographic estimation
of focusing velocity.
)enables the computation of reflections traveltimes
independent of depth-mapping.
This separation allows
the focusing and mapping
steps to be performed sequentially
even in the presence of complex velocity functions,
that otherwise would ``require'' depth migration.
The traveltimes satisfying the transformed eikonal equation
can be numerically evaluated by solving the associated
ray tracing equations.
The application of Fermat's principle
leads to the expression of linear relationships
between perturbations in traveltimes and
perturbations in focusing velocity.
This linearization, in conjunction with ray tracing,
can be used for a tomographic estimation
of focusing velocity.
Time-domain anisotropic processing in arbitrarily inhomogeneous media (ps.gz 203K) (pdf 188K) (src 25K)
Alkhalifah T., Fomel S., and Biondi B.
In transversely isotropic media with a vertical axis of symmetry
(VTI media), we can represent the image in
vertical time, as opposed to depth, thus eliminating
the inherent ambiguity of resolving the vertical P-wave velocity from
surface seismic data. In this new 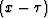 -domain, the raytracing and eikonal equations are
completely independent of the vertical P-wave velocity, on the condition that the
ratio of the vertical to normal-moveout (NMO) P-wave velocity (
-domain, the raytracing and eikonal equations are
completely independent of the vertical P-wave velocity, on the condition that the
ratio of the vertical to normal-moveout (NMO) P-wave velocity ( ) is laterally invariant.
Practical size
departures of
) is laterally invariant.
Practical size
departures of  from lateral homogeneity affect traveltimes only slightly. As a result, for all
practical purposes, the VTI equations in the
from lateral homogeneity affect traveltimes only slightly. As a result, for all
practical purposes, the VTI equations in the 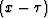 -domain become dependent on only two parameters in
laterally inhomogeneous media: the NMO velocity for a horizontal reflector, and
an anisotropy parameter,
-domain become dependent on only two parameters in
laterally inhomogeneous media: the NMO velocity for a horizontal reflector, and
an anisotropy parameter,  . An acoustic wave equation in the
. An acoustic wave equation in the 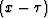 -domain is also independent
of the vertical velocity. It includes an unsymmetric Laplacian operator to accommodate the unbalanced
axis units in this new domain.
In summary, we have established the basis for a full inhomogeneous
time-processing scheme in VTI media that is dependent on only
v and
-domain is also independent
of the vertical velocity. It includes an unsymmetric Laplacian operator to accommodate the unbalanced
axis units in this new domain.
In summary, we have established the basis for a full inhomogeneous
time-processing scheme in VTI media that is dependent on only
v and  , and independent of the vertical P-wave velocity.
, and independent of the vertical P-wave velocity.
Huygens wavefront tracing: A robust alternative to conventional ray tracing (ps.gz 606K) (pdf 872K) (src 109K)
Sava P. and Fomel S.
We present a method of ray tracing that is based on a system of
differential equations equivalent to the eikonal equation, but formulated
in the ray coordinate system. We use a first-order discretization scheme
that is interpreted very simply in terms of the Huygens' principle. The
method has proved to be a robust alternative to conventional ray tracing,
while being faster and having a better ability to penetrate the shadow
zones.
A variational formulation of the fast marching eikonal solver (ps.gz 565K) (pdf 742K) (src 201K)
Fomel S.
I exploit the theoretical link between the eikonal equation and
Fermat's principle to derive a variational interpretation of the
recently developed method for fast traveltime computations. This
method, known as fast marching, possesses remarkable computational
properties. Based originally on the eikonal equation, it can be
derived equally well from Fermat's principle. The new variational
formulation has two important applications: First, the method can be
extended naturally for traveltime computation on unstructured
(triangulated) grids. Second, it can be generalized to handle other
Hamilton-type equations through their correspondence with
variational principles.
Implementing the fast marching eikonal solver: Spherical versus Cartesian coordinates (ps.gz 1676K) (pdf 1300K) (src 35K)
Alkhalifah T. and Fomel S.
Spherical coordinates are a natural orthogonal system to
describe wavefronts emanating from a point source. While a regular
grid distribution in the Cartesian coordinate system tends to
undersample the wavefront description near the source (the highest
wavefront curvature) and oversample it away from the source,
spherical coordinates, in general, provide a more balanced grid
distribution to characterize such wavefronts. Our numerical
implementation confirms that the recently introduced fast marching
algorithm is both a highly efficient and an unconditionally stable
eikonal solver. However, its first-order approximation of traveltime
derivatives can induce relatively large traveltime errors for waves
propagating in a diagonal direction with respect to the coordinate
system. Examples, including the infamous Marmousi model, show that a
spherical coordinate implementation of the method results in far
fewer errors in traveltime calculation than the conventional
Cartesian coordinate implementation, and with practically no loss in
computational advantages.
Fast-marching eikonal solver in the tetragonal coordinates (ps.gz 161K) (pdf 251K) (src 40K)
Sun Y. and Fomel S.
Accurate and efficient traveltime calculation is an important topic in
seismic imaging.
We present a fast-marching eikonal solver in the tetragonal coordinates (3-D)
and trigonal coordinates (2-D), tetragonal (trigonal) fast-marching
eikonal solver (TFMES), which can significantly reduce the first-order
approximation error without greatly increasing the computational
complexity. In the trigonal coordinates, there are six equally-spaced points
surrounding one specific point and the number is twelve in the
tetragonal coordinates, whereas the numbers of points are four and six
respectively in the Cartesian coordinates. This means that the local
traveltime updating space is more densely sampled in the tetragonal (
or trigonal) coordinates, which is the main reason that TFMES is more
accurate than its counterpart in the Cartesian coordinates. Compared with
the fast-marching eikonal solver in the polar coordinates, TFMES is
more convenient since it needs only to transform the velocity model from
the Cartesian to the tetragonal coordinates for one time. Potentially,
TFMES can handle the complex velocity model better than the polar
fast-marching solver. We also show that TFMES can be completely derived
from Fermat's principle. This variational formulation implies that the
fast-marching method can be extended for traveltime computation on other
nonorthogonal or unstructured grids.
A second-order fast marching eikonal solver (ps.gz 136K) (pdf 306K) (src 17K)
Rickett J. and Fomel S.
The fast marching method Sethian (1996) is widely used for solving the
eikonal equation in Cartesian coordinates.
The method's principal advantages are: stability,
computational efficiency, and algorithmic simplicity.
Within geophysics, fast marching traveltime
calculations Popovici and Sethian (1997) may be used
for 3-D depth migration or velocity analysis.
...
AMO
Amplitude preserving offset continuation in theory Part 1: The offset continuation equation (ps.gz 73K) (pdf 92K) (src 16K)
Fomel S.
This paper concerns amplitude-preserving kinematically equivalent
offset continuation (OC) operators. I introduce a revised partial
differential OC equation as a tool to build
OC operators that preserve offset-dependent reflectivity in prestack
processing. The method of characteristics is applied to reveal the
geometric laws of the OC process. With the help of geometric
(kinematic) constructions, the equation is proved to be
kinematically valid for all
offsets and reflector dips in constant velocity media.
In the OC process,
the angle-dependent reflection coefficient is preserved, and the
geometric spreading factor is transformed in accordance with the laws
of geometric seismics independently of the reflector curvature.
Amplitude preserving offset continuation in theory Part 2: Solving the equation (ps.gz 102K) (pdf 126K) (src 46K)
Fomel S.
I consider an initial value problem for the offset continuation (OC)
equation introduced in Part One of this paper (SEP-84). The solutions
of this problem create integral-type OC operators in the time-space
domain. Moving to the frequency-wavenumber and log-stretch domain, I
compare the obtained operators with the well-known Fourier DMO
operators. This comparison links the theory of DMO with the advanced
theory of offset continuation.
Azimuth moveout: the operator parameterization and antialiasing (ps.gz 629K) (pdf 987K) (src 38K)
Fomel S. and Biondi B. L.
A practical implementation of azimuth moveout (AMO) must be both
computationally efficient and accurate. We achieve computational
efficiency by parameterizing the AMO operator with the help of a
transformed midpoint coordinate system. To achieve accuracy, the AMO
operator needs to be carefully designed for antialiasing. We propose
a modified version of Hale's antialiasing algorithm, which switches
between interpolation in time and interpolation in space depending on
the operator dips. The method is applicable to a vide variety of
integral operators and compares favorably with the triangle filter
technique. A simple synthetic example tests the applicability of the
method to the AMO case.
Application of azimuth moveout to the coherent partial stacking of a 3-D marine data set (ps.gz 1081K) (pdf 1080K) (src 20K)
Biondi B., Fomel S., and Chemingui N.
The application of azimuth moveout (AMO) to a marine
3-D data set shows that
by including AMO in the processing flow
the high-frequency steeply-dipping energy
can be better preserved
during partial stacking over a range of offsets and azimuths.
Since the test data set requires 3-D prestack depth migration
to handle strong lateral velocity variations,
the results of our tests support the applicability
of AMO to prestack depth imaging problems.
Amplitude preservation for offset continuation: Confirmation for Kirchhoff data (ps.gz 37K) (pdf 9K) (src 9K)
Fomel S. and Bleistein N.
Offset continuation (OC) is the operator that transforms common-offset
seismic reflection data from one offset to another. Earlier papers by
the first author presented a partial differential equation in midpoint
and offset to achieve this transformation. The equation was derived
from the kinematics of the continuation process. This derivation is
equivalent to proposing the wave equation from knowledge of the
eikonal equation. While such a method will produce a PDE with the
correct traveltimes, it does not guarantee that the amplitude will be
correctly propagated by the resulting second-order partial
differential equation. The second author (with J. K. Cohen) proposed
a dip moveout (DMO) operator for which a verification of amplitude
preservation was proven for Kirchhoff data. It was observed that the
solution of the OC partial differential equation produced the same DMO
solution when specialized to continue data to zero offset.
Synthesizing these two approaches, we present here a proof that the
solution of the OC partial differential equation does propagate
amplitude properly at all offsets, at least to the same order of
accuracy as the Kirchhoff approximation. That is, the OC equation
provides a solution with the correct traveltime and correct
leading-order amplitude. ``Correct amplitude'' in this case means
that the transformed amplitude exhibits the right geometrical
spreading and reflection-surface-curvature effects for the new offset.
The reflection coefficient of the original offset is preserved in this
transformation. This result is more general than the earlier results
in that it does not rely on the two-and-one-half dimensional
assumption.
Azimuth moveout for 3-D prestack imaging (ps.gz 1267K) (pdf 1246K) (src 37K)
Biondi B., Fomel S., and Chemingui N.
We introduce a new partial prestack-migration operator,
named Azimuth MoveOut (AMO),
that rotates the azimuth and modifies the offset of 3-D prestack data.
AMO can improve the accuracy and reduce the computational
cost of 3-D prestack imaging.
We have successfully applied AMO to the partial stacking
of a 3-D marine data set
over a range of offsets and azimuths.
Our results show that
when AMO is included in the processing flow,
the high-frequency steeply-dipping energy
is better preserved
during partial stacking
than when conventional partial-stacking methodologies are used.
Because the test data set requires 3-D prestack depth migration
to handle strong lateral variations in velocity,
the results of our tests support the applicability
of AMO to prestack depth-imaging problems.
AMO is defined as the cascade of a 3-D prestack imaging
operator with the corresponding 3-D prestack modeling.
To derive analytical expressions for the AMO impulse response,
we used both constant-velocity DMO and its inverse,
as well as constant-velocity prestack migration and modeling.
Because 3-D prestack data is typically irregularly sampled
in the surface coordinates,
AMO is naturally applied as an integral operator in the
time-space domain.
The AMO impulse response is a skewed saddle
surface in the time-midpoint space.
Its shape depends on the amount
of azimuth rotation and offset continuation to be applied to the data,
but it is velocity independent.
The AMO spatial aperture, on the contrary,
does depend on the minimum velocity.
When the azimuth rotation is small (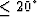 ),
the AMO impulse response is compact
and its application as an integral operator is inexpensive.
Implementing AMO as an
integral operator is not straightforward because
the AMO saddle may have a strong curvature
when it is expressed in the usual midpoint coordinates.
To regularize the AMO saddle,
we introduce
an appropriate transformation of the midpoint axes
that leads to an effective implementation.
),
the AMO impulse response is compact
and its application as an integral operator is inexpensive.
Implementing AMO as an
integral operator is not straightforward because
the AMO saddle may have a strong curvature
when it is expressed in the usual midpoint coordinates.
To regularize the AMO saddle,
we introduce
an appropriate transformation of the midpoint axes
that leads to an effective implementation.
Velocities
On nonhyperbolic reflection moveout in anisotropic media (ps.gz 86K) (pdf 113K) (src 22K)
Fomel S. and Grechka V.
The famous hyperbolic approximation of P-wave reflection moveout is
strictly accurate only if the reflector is a plane, and the medium is
homogeneous and isotropic. Heterogeneity, reflector curvature, and
anisotropy are the three possible causes of moveout
nonhyperbolicity at large offsets. In this paper, we analyze the
situations where anisotropy is coupled with one of the other two
effects. Using the weak anisotropy assumption for transversely
isotropic media, we perform analytical derivations and comparisons.
Both the case of vertical heterogeneity and the case of a curved
reflector can be interpreted in terms of an effective anisotropy,
though their anisotropic effects are inherently different from the
effect of a homogeneous transversely isotropic model.
Migration and velocity analysis by velocity continuation (ps.gz 504K) (pdf 529K) (src 41K)
Fomel S.
Residual and cascaded migration can be described as a continuous
process of velocity continuation in the post-migration domain. This
process moves reflection events on the migrated seismic sections
according to changes in the migration velocity. Understanding the laws
of velocity continuation is crucially important for a successful
application of migration velocity analysis. In this paper, I derive the kinematic
laws for the case of prestack residual migration from simple
trigonometric principles. The kinematic laws lead to dynamic theory
via the method of characteristics. The main theoretical result is a
decomposition of prestack velocity continuation into three different
components corresponding to residual normal moveout, residual dip
moveout, and residual zero-offset migration. The contribution and
properties of each of the three components are analyzed separately.
Residual migration in VTI media using anisotropy continuation (ps.gz 88K) (pdf 131K) (src 13K)
Alkhalifah T. and Fomel S.
We introduce anisotropy continuation as a process which relates
changes in seismic images to perturbations in the anisotropic medium
parameters. This process is constrained by two kinematic equations,
one for perturbations in the normal-moveout (NMO) velocity and the
other for perturbations in the dimensionless anisotropy parameter
 . We consider separately the case of post-stack migration and
show that the kinematic equations in this case can be solved
explicitly by converting them to ordinary differential equations by
the method of characteristics. Comparing the results of kinematic
computations with synthetic numerical experiments confirms the
theoretical accuracy of the method.
. We consider separately the case of post-stack migration and
show that the kinematic equations in this case can be solved
explicitly by converting them to ordinary differential equations by
the method of characteristics. Comparing the results of kinematic
computations with synthetic numerical experiments confirms the
theoretical accuracy of the method.
Velocity continuation by spectral methods (ps.gz 1411K) (pdf 1323K) (src 25K)
Fomel S.
I apply Fourier and Chebyshev spectral methods to derive accurate
and efficient algorithms for velocity continuation. As expected,
the accuracy of the spectral methods is noticeably superior to that
of the finite-difference approach. Both methods apply a
transformation of the time axis to squared time. The Chebyshev
method is slightly less efficient than the Fourier method, but has
less problems with the time transformation and also handles
accurately the non-periodic boundary conditions.
Velocity continuation in migration velocity analysis (ps.gz 1566K) (pdf 0K) (src 24K)
Fomel S.
Velocity continuation can be applied to migration velocity
analysis. It enhances residual NMO correction by properly taking
into account both vertical and lateral movements of reflectors
caused by the change in migration velocity. I exemplify this fact
with simple data tests.
Software
A generic NMO program (ps.gz 59K) (pdf 0K) (src 33K)
Fomel S., Crawley S., and Clapp R.
Jon Claerbout's books Processing versus Inversion
1992b and Three-dimensional
Filtering 1994 list normal moveout (NMO)
among the basic linear operators. Indeed, the NMO transformation plays
a kernel role in many applications of geophysical data processing,
from simple CMP stacking to prestack migration and velocity
analysis. The importance of this role increases with the development
...
Simple linear operators in Fortran 90 (ps.gz 39K) (pdf 0K) (src 10K)
Fomel S. and Claerbout J.
A linear operator maps an input vector to an output vector. In the
adjoint mode, the mapping direction is reverse. The simplest
implementation of this idea is a minimal interface
operator( adj, add, model, data), where the logical variable
adj defines adjoint or forward mode, and variable
add defines whether the output of the program
should be added to the previous value of the corresponding actual
argument. The minimal interface is the ``mathematical'' connection to
operators as objects. To provide the ``geophysical'' connection,
we need to initialize an operator with the arguments that ...
``SEP'' module: A Fortran-90 interface to SEPlib (ps.gz 14K) (pdf 0K) (src 10K)
Fomel S.
A simplified interface to SEPlib is implemented with a Fortran-90
module.
Empowering SEP's documents (ps.gz 186K) (pdf 0K) (src 14K)
Fomel S., Schwab M., and Schroeder J.
The arrival of LATEX2e at SEP enhanced our LATEX typesetting system
and led us to overhaul SEP's customized macros. The revised
system enables us to use the latex2html script
Drakos (1996) to publish our documents routinely on the Internet.
Additionally, we improved the communication between a document's
makefile and its corresponding LATEX file. Finally, we replaced a
gigantic c-shell script (texpr) that governed SEP's entire
document processing, by a set of small Perl scripts. These Perl
...
Reproducible research - results from SEP-100 (ps.gz 8K) (pdf 0K) (src 2K)
Prucha M. L., Clapp R. G., Fomel S., Claerbout J., and Biondi B.
SEP has been striving to create reproducible research for many years.
Our first attempts at reproducible documents began with the introduction
of interactive documents Claerbout (1990). We then moved on
to putting SEP reports on CDROMs and using ``cake'' Nichols and Cole (1989)
so that the results could be recreated using the author's own processing
flow. Later we updated to the GNU make system Schwab and Schroeder (1995).
Now SEP reports are available online and can be downloaded.
...


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: About this document ...
Up: Table of Contents
Stanford Exploration Project
11/14/2000
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)