![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
Monte Carlo automatic velocity picks (ps 1424K) (src 4127K)
Lumley D. E.
I develop a method for making automatic
velocity picks from velocity semblance scans, using a Monte Carlo
nonlinear fitting technique. Given a single velocity semblance scan,
random interval velocity models are generated by performing many
Monte Carlo random walks. For each trial random interval velocity model, the
corresponding rms velocity is calculated, and the semblance
is integrated along the trial rms velocity path through the velocity
scan. After several random walks, one interval velocity model, and
its associated rms velocity function, is retained as the global best
fit to the velocity scan which maximizes semblance. The result is
a nonlinearly optimal rms velocity function,
and an associated geologically reasonable interval velocity model,
at each surface CMP location. I tested the method on 300 marine CMP
gathers, and the Monte Carlo picks gave reasonable rms and interval
velocity models which enhanced the stacked and prestack migrated images.
Plumes: Response of time migration to lateral velocity variation (ps 234K) (src 11423K)
Black J. L., Bevc D., Brzostowski M. A., Mo L., and Palacharla G.
Lateral velocity variation causes time migration to misposition events.
Black and Brzostowski 1993 quantify this error by developing a
first order theory for the positioning error in terms of x and t.
The response of a point diffractor in a medium with a simple lateral
velocity variation is a distinctive cusp-like shape that we call a ``plume''.
The nature of the plume is revealed by making two geometrical constructions
based upon point diffractor ray-tracing: superposition of semicircles
and summation along hyperbolas. The plume shapes derived by these two
techniques are consistent with results obtained by
migrating synthetic
point diffractors using the Kirchhoff, Stolt, and Gazdag
time migration methods.
The shapes of these plumes resemble
those predicted by Black and
Brzostowski's simple first-order theory, but the actual plumes are less
symmetric than the predictions.
Thus a higher-order theory is needed.
Migration velocity dependence of plumes (ps 377K) (src 11383K)
Black J. L., Bevc D., and Palacharla G.
Changing the migration velocity causes the response of time
migration to a point diffractor beneath a lateral velocity variation
to evolve. At the extremes of migration velocity,
the image is either
fully undermigrated or fully overmigrated. Between
these extremes, there is the mixture of overmigration and undermigration
that leads to ``plume'' responses. As the velocity is changed, these
plumes transform and rotate in a systematic manner. A simple first-order
theory of plume velocity dependence explains some, but not all,
of the observed behavior.
Migration of crosswell seismic data (ps 816K) (src 3844K)
Mo L.
Crosswell seismic survey has proven to be an effective,
high-resolution method of reservoir characterization.
However, its application has been mainly confined to transmission
traveltime tomography, even though extensions have
recently been made to reflection imaging.
This paper describes the application of
reverse-time wavefield extrapolation coupled with
the excitation-time imaging condition to the migration
of crosswell seismic common-shot profiles.
I have applied fourth-order-in-time, tenth-order-in-space
finite differencing to perform the crosswell seismic modeling of
the two-way acoustic wave equation.
During the migration wavefield backpropagation, I gradually drop
the order of finite differencing to the second-order
near the recording boundary for the derivative
perpendicular to the recording boundary, so that the numerical
computation conforms to physical wave phenomena.
Modeling and migration are based on the geometry of
a true field survey.
This method successfully models high frequency
crosswell seismic wavefields.
Migration of one common-shot profile gives a very clear reflectivity
image. Vertical resolution up to
a half wavelength and horizontal resolution as governed by the
first Fresnel zone width have been realized.
At the end, the paper presents some suggestions
to facilitate field data migration,
which include removal of tube waves and wavefield separation.
Gaussian beam migration (ps 868K) (src 1491K)
Mo L.
This paper reports on my use of Gaussian beam wave propagation
theory to downward
continue all the frequency components of individual surface
recorded wavefield traces (point sources) into the subsurface.
According to the Huygens secondary point source principle,
the surface recorded wavefields
can be regarded as a series of point sources.
The theory of Gaussian beam wave propagation asserts that
asymptotic high frequency wavefield components propagate along rays,
of which the wavefronts are parabolas and the amplitude profiles
overriding the ray paths
are Gaussian functions decaying away from the central ray paths.
With my method, Gaussian beam wave propagation is implemented
in the space-frequency domain.
Poststack and prestack common-shot profile migration
are accomplished by applying the
corresponding imaging condition to the downward continued
Gaussian beam wavefields in the frequency domain.
The surface seismograms are migrated separately,
and the migration process finishes by summing
the contributions of all surface recorded traces to obtain the
subsurface reflectivity image.
This migration scheme combines the advantages of
complete wave equation migration and ray tracing based migration.
Tests with synthetic data show that the Gaussian beams evaluated
along only seventeen rays from each surface seismogram location
can image a fairly complex velocity and reflectivity model.
Numerical analysis of 
migration (ps 55K) (src 6K)
Mo L.
For the constant velocity 15-degree space-frequency (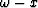
)
time migration algorithm, the parabolic approximation of
the exact one-way wave equation causes undermigration,
and the Crank-Nicolson numerical method that is used to solve the
diffraction equation causes overmigration.
However, the modified wave equation that the numerical
solution actually satisfies for the diffraction equation
shows that the trace spacing interval plays a larger role than
the depth step size of downward continuation
in determining the accuracy of the numerical solution.
Fast anti-aliased Kirchhoff migration and modeling (ps 260K) (src 265K)
Bevc D. and Claerbout J.
We describe an optimized Kirchhoff migration and modeling routine which
handles the problem of operator aliasing. Slight modifications of
this algorithm could be useful for velocity analysis, pre-stack
migration and DMO.
Several Kirchhoff routines are presented in SEP73. The simplest routines
Claerbout (1992b) are tutorial and do not address the problem
of operator aliasing. A more elaborate routine which overcomes the
aliasing problem
...
Unitary operators in inversion (ps 39K) (src 4K)
Claerbout J. F.
Geophysical model building springs from
a variety of related formulas ranging from inversion to back projection.
When the number of unknowns is huge,
as when we seek an image of the earth's reflectivity,
then using the conjugate operator
(also known as back projection or migration)
is always a possible starting technique.
The conjugate operator can generally be improved
by any transformation that pushes it towards a unitary operator.
Unitary operators play an important role in imaging practice
...
Least-squares Kirchhoff migration (ps 181K) (src 222K)
Cole S. and Karrenbach M.
Slant stacks of finite-aperture data contain artifacts
that are a result of the limited aperture. Resolution in the
transform domain is also adversely affected by the finite aperture.
Clement Kostov (Kostov, 1990), using least-squares inverse
operators formulated by Beylkin (1987), developed least-squares
slant stack transforms that compensate for the limited
aperture, reducing artifacts and improving resolution.
These least-squares transforms are best implemented in the frequency
domain, where a separate, small least-squares problem can be
constructed for each frequency.
...
Least squares imaging, datuming, and interpolation using the wave equation (ps 765K) (src 3066K)
Ji J.
Though the continuous wave equation defines a unitary operator,
many operators based on it are not unitary
because many approximations are made to be implemented numerically
in finite and discrete space.
The nonunitary property of the operators
produces many artifacts in the solution space when is applied
to data that was generated by a continuous unitary operator,
such as real seismic data.
This paper presents a method of reducing these kinds of artifacts
in migration, datuming, and interpolation
by using the technique of a least-squares optimization.
Reverse-time migration as the conjugate of forward modeling (ps 224K) (src 4934K)
Ji J.
This paper presents a reverse-time migration algorithm
as the conjugate of the forward time-extrapolation modeling.
The conjugate operator is obtained by formulating
the forward operator explicitly and by transposing the forward operator.
The algorithm is tested by a numerical experiment for a 1-D layered model.
A method to suppress artifacts, which are caused
by the intrinsic non-unitary property of the operator,
is introduced using the least-squares optimization technique.
A Gazdag routine passing the dot-product test (ps 40K) (src 3K)
Claerbout J. F.
We examine differential equations
of the form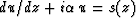 
and find the pair of conjugate operators
relating s(z) and u(z=0).
This leads up to a Gazdag subroutine
that passes the dot-product test.
Kirchhoff wave-equation datuming with irregular acquisition topography (ps 1066K) (src 4180K)
Bevc D.
Seismic data gathered on land is distorted by
irregular acquisition topography. Most seismic imaging algorithms are applied
to data which is shifted to a planar datum. In regions of mild topography
a static shift is adequate to perform this transformation,
however as the
necessary shift increases in magnitude, the static approximation becomes
inadequate. In this situation a procedure based on
wave-equation extrapolation is more appropriate than static shift.
After describing the Kirchhoff datuming algorithm I apply it to a deep-water
marine data set and to synthetic land data.
The land data examples demonstrate that wave-equation
datuming is more appropriate than static shift in regions of large topographic
relief.
Phase shift datuming and migration from an irregular surface (ps 214K) (src 561K)
Ji J. and Claerbout J.
We present a phase shift datuming and migration algorithm
for the data acquired on a nonflat surface.
First of all, we formulate the exploding reflector modeling scheme
for a nonflat recording surface.
Then, the migration scheme is found
as the conjugate operator of the modeling operator.
In order to get the correct migration and datuming operators,
the forward modeling must be physically reasonable because
the conjugate operators are strongly dependent on the forward modeling operator.
The artifacts caused by the non-unitary property of the operators
can be reduced by a least-squares optimization technique.
Datuming by wavefield extrapolation (ps 1399K) (src 4131K)
Mo L.
This paper proposes a method of datuming that uses
the exact two-way acoustic wave equation to do
the wavefield extrapolation along with depth migration.
Datuming is the process used to derive the wavefields at one datum
from those at another datum.
Poststack and prestack datuming regard
the surface recorded wavefields as containing
only subsurface primary reflections.
In accord with this assumption, this paper points out that the surface
recorded seismograms are the wavefields recorded at
the earth surface, which is regarded as an absorbing boundary.
According to the Huygens secondary-point-source principle,
the surface recorded wavefields
can also be regarded as a series of point sources.
The datuming procedure I propose
is implemented in the space-time domain
by the finite-difference method.
The recorded wavefields are taken as boundary conditions (sources)
to drive the wave equation along the time axis in a rectangular
strip containing the input and output datums.
The desired wavefields
at the output datum are the history wavefields at the output datum,
with the four sides designed as absorbing boundaries.
This method can handle any velocity variation between the two datums.
In practical situations, one of the two datums is an irregular surface.
This paper shows both upward and downward,
poststack and prestack wave equation datuming.
Tests with synthetic data show good results.
The method has the potential for application
to corrections of land data static
and to migration in complex velocity areas.
Wave-equation datuming in variable velocity media (ps 481K) (src 4680K)
Popovici A. M.
Wave equation datuming represents the process of
upward or downward continuing seismic data to a new
reference surface. Usually datuming algorithms are based on
the Kirchhoff integral solution to the wave equation.
I present a new wave-equation datuming
algorithm based on wavefield continuation through
Fourier methods which handles laterally and depth
varying velocity models. I show datuming results
for different velocity models and the
migration results before and after datuming.
Green's function traveltime interpolation (ps 742K) (src 1952K)
Lumley D. E.
Green's function traveltime fields are useful for Kirchhoff depth migration
and inversion applications, and for tomographic velocity inversion.
However, in 2-D, and especially 3-D, traveltimes become increasingly
computationally expensive. Based on the physical continuity of
(first arrival) traveltimes, I derive a
least squares expression from the ray theoretic eikonal equation,
which allows for the interpolation of known Green's function traveltime
functions from several surface source positions, to one or more Green's
function traveltime functions at intermediate arbitrary source positions.
The least squares equation is parameterized in terms of the traveltime
gradient, and is solved by standard weighted least-squares techniques
and Singular Value Decomposition, and then integrated up to traveltime
directly.
For a 2-D (3-D) geometry, at least two (three) traveltime fields must
be known in order to interpolate the unknown source traveltime field.
I test the theory and algorithm on a constant velocity model, constant
velocity gradient model, and the complex 2-D structural velocity model
of Marmousi. The results are very encouraging to date, although some
sparse numerical instability in the calculation of the traveltime gradient
fields must be overcome in order to be of practical use.
Wave equation resampling of unevenly spaced traces (ps 351K) (src 4160K)
Zhang L. and Claerbout J.
Many seismic data processing algorithms require that input data have
uniform sampling intervals both in time and in space.
However, in reality, difficulties in positioning
the sources and receivers may cause the spatial sampling intervals
to vary from place to place. If the variations of the sampling intervals
are too large to be acceptable for data processing, seismic traces
have to be resampled.
Because seismic data are almost always sampled uniformly in time,
conventional methods perform the spatial resampling along each constant
...
Modeling reflections from the Austin Chalk - a practical application of azimuthal anisotropy (ps 1069K) (src 1810K)
Karrenbach M., Nichols D., and Muir F.
If a rock has elastic properties that vary with azimuth, then
reflections from such a rock will likewise. We examine a simple situation
where a homogeneous model material - representing a shale - overlies
another homogeneous model material which simulates an isotropic chalk
matrix and a set of vertical fractures with constant azimuth. Our modeling
illustrates the small variability in azimuthal reflectivity as the amount of
fracturing is increased, and also how reflection strength is affected by
the nature of the fluid inclusion - gas or liquid.
``Plug and Play'' wave equation modules (ps 2991K) (src 10314K)
Karrenbach M.
Prestack modeling and migration programs can share a common structure.
I outline this structure in the common shot domain for scalar or vector
fields of any degree of anisotropy.
The generality of the code is striking, and works for any combination of space
and vector dimensionality.
The actual pieces of FORTRAN 90 code are shown as listings
in the paper.
The advantage of this modeling strategy is that there exists
only one piece of code that has to be maintained.
The various media types are declared in the main program as single variables
(objects), and they all use the same subroutines.
The mathematical formulation is apparent in the notation and the modeling code
can easily handle the usual finite differences or
pseudo spectral cases or any combination.
Reverse time migration is accomplished by using the same set of
subroutines, conjugating of the modeling operation and
additionally calculating the gradient (``imaging'').
There is a trade-off between performance and common structure when,
for example,
the Laplacian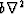 
could be used instead of 
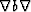in constant velocity models.
Wavefront propagation by local ray-tracing (ps 6344K) (src 7223K)
Zhang L.
I develop a new wavefront-propagation method for calculating
the traveltimes and geometrical amplitudes of seismic waves in a
two-dimensional velocity model. The method assumes that the given velocity
field is specified on a grid formed by regular triangular cells and that
the velocity within each triangular cell varies linearly. These
assumptions lead to
a continuous representation of the velocity field.
Five attributes are assigned to the wavefront at each grid point.
They are traveltime, traveltime gradient, take-off angle,
curvature radius of wavefront and geometric spreading factor.
The attributes of a wavefront at one corner of a triangular cell
are calculated from the attributes of wavefronts at other two
corners by propagating the local circular wavefront through
the triangular cell under the guidance of local rays.
Starting from a given source position, these local computations proceed
on an expanding half hexagonal ring. The new method computes the traveltimes of
multiple arrivals by disassembling
a multi-valued traveltime field into several single-valued fields, and then
computing each of them separately. The method is evaluated with several
synthetic velocity models, and its accuracy is checked with both
analytical solutions and wave equation modeling.
Elastic constants of transversely isotropic media from constrained aperture traveltimes (ps 633K) (src 656K)
Michelena R. J.
The elastic constants that control P- and SV-wave propagation
in a transversely isotropic media can be estimated by using
P- and SV-wave traveltimes from either cross-well or VSP
geometries. The procedure consists of two steps. First, elliptical
velocity models are used to fit the traveltimes near one axis.
The result is four elliptical parameters that represent
direct and normal moveout velocities near the chosen axis
for P- and SV-waves. Second, the elliptical parameters are used to
solve a system of four equations and four unknown elastic constants.
The system of equations is solved analytically yielding
simple expressions for the elastic constants as a function of
direct and normal moveout velocities.
For SH-waves the estimation of the corresponding elastic
constants is easier because the phase
velocity is already elliptical.
The procedure, introduced for homogeneous media,
can be generalized to heterogeneous media by using
tomographic techniques.
The technique is illustrated with synthetic examples in a homogeneous
medium.
Anelliptic approximations for TI media (ps 2309K) (src 4145K)
Dellinger J., Muir F., and Karrenbach M.
Homogeneous scalar isotropy can be completely specified by a single velocity.
Elliptical anisotropy with a vertical symmetry axis requires
two velocities, vertical and horizontal.
For some problems these two velocities may not be enough.
In particular, because vertical scale is unknown for surface-recorded data
the vertical velocity in elliptical anisotropy gains nothing over isotropy.
We introduce two successive scalar anisotropic approximations beyond elliptical
anisotropy which can be used when more independent parameters are needed
but the full complexity of transverse isotropy is unnecessary.
Both approximations take the form of simple rational polynomials.
We call them anelliptic approximations to indicate that although
they are not elliptical,
they do share some of elliptical anisotropy's useful properties.
We show examples of how both anelliptic approximations
can be used to fit transversely isotropic wave modes with acceptable accuracy.
The first anelliptic approximation is specified by three parameters:
vertical velocity, surface NMO velocity, and true horizontal velocity.
The first two velocity parameters determine the near-vertical
paraxial behavior, which is elliptic.
The second anelliptic approximation is specified by four parameters:
vertical velocity, surface NMO velocity, true horizontal velocity,
and borehole NMO velocity.
The first anelliptic approximation occurs as a special case.
To a good approximation,
both of the anelliptic approximations have identical forms in
the group-velocity and dispersion-relation domains
and converting between the two domains is trivial.
The anelliptic velocity parameters are convenient and robust because
of their close relationship to standard geophysical measurements.
We also show how Dix's equations for stack-moveout velocities
can be interpreted in terms of a paraxial layer group, and how
this formulation naturally leads to an anelliptic extension of
Dix's equations.
The anelliptic Dix equations encompass nonhyperbolic moveout both
as a result of intrinsic anisotropy and ray bending at layers.
Estimation of elastic specular reflectivity by Kirchhoff prestack depth migration: WKBJ least-squares theory (ps 85K) (src 26K)
Lumley D. E.
Estimation of elastic specular reflectivity from seismic reflection data
is important in that it may provide crucial information about
subsurface physical
properties related to lithology, rock physics, pore-fluid content, and
physical states. I derive a generalized least-squares solution for
elastic reflectivity in terms of local seismic wavefield displacement vectors.
Solutions for the local wavefields are derived as representation integrals
over surface source and receiver displacement fields, weighted by a
WKBJ approximate Green's tensor. The resulting integral solution is a
vector analogy of the Kirchhoff-Rayleigh-Sommerfeld integrals for scalar waves.
In particular, I give explicit formulas for the least-squares evaluation of the
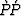and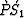 
elastic specular reflection coefficients.
The inertia tensor in elastic wave modeling (ps 37K) (src 2K)
Muir F.
The homogeneous equivalent to a fine-layered, heterogeneous elastic medium
may need a frequency-dependent, anisotropic inertia tensor if it is to be
dynamically equivalent in a useful sense. The elastic and inertial matrices
that make up this equation would likely not commute, and there would be no
Christoffel-like equation. This difficulty is resolved by a local
transformation of the field variable from displacement to an energy form.
This inertia tensor is shown, by analogy, to be physically reasonable.
Wavelets and seismic processing (ps 262K) (src 769K)
Abma R. and Muir F.
Various wavelet transforms are compared and the fundamentals of
wavelet transforms are examined. While wavelet transforms
appear to provide much promise for signal processing, we found no
apparent application other than some limited data compression
possibilities. The absence
of useful properties within the transformed domain, such
as the derivative property in the Fourier transform,
account for the present lack of applications.
Transformation of discrete arrays by Daubechies wavelets (ps 1100K) (src 1815K)
Schwab M.
Wavelet transformation, analogously
to fast Fourier transformation,
turns a discrete vector of length N into a
vector of N coefficients, which scale the transformation's
base functions. It is a linear operation
which can be efficiently implemented as a recursion.
Requiring the base function of the transformation
to be orthogonal and approximative yields
a set of constraining equations for discrete wavelets.
Daubechies wavelet filter coefficients are the
minimum phase solutions of this nonlinear equation set.
I implemented a pyramidal algorithm which performs the
transformation based on Daubechies wavelets of lengths
from 4 to 20 samples.
In the electronic version of this report, interactive figures allow
readers to explore the transformation by submitting their own
input and choosing the wavelet's length.
By compressing and
recovering a photograph of a face, I demonstrate the conditions
for a successful wavelet compression; the matrix representation
of the picture in the wavelet space
is sparse and samples with small values can be neglected without
affecting essential features of the uncompressed picture.
Seismic data render rather densely in the wavelet domain.
Finally, lacking clear criteria to define seismic data quality, a
compression scheme based on data reduction does not seem to be practical.
A more promising seismic application of wavelet transformation is
interpolation.
As with fast Fourier transformation, I utilize
discrete wavelet transformation for interpolation of regularly sampled
seismic traces by padding zeroes.
Wavefield extrapolation in heterogeneous media using the LITWEQ method (ps 55K) (src 12K)
Mujica D. L.
Time migration algorithms have the disadvantage of erroneously handling
lateral velocity variations, even if the correct velocity is provided (Hatton et al., 1981).
Additionally, algorithms based on the one-way wave equation cannot
handle steep dips correctly. Depth migration seems to be
the answer to time migration weaknesses. This explains why it is
necessary to develop depth migration algorithms. Li (1986),
presents a theoretical model that he calls Linearly Transformed
Wave Equation (LITWEQ) to do migration in lateraly varying media.
However, it was only implemented
...
Dip-Moveout processing: A Tutorial. DMO basics and DMO by Fourier transform (ps 411K) (src 364K)
Popovici A. M.
As a Teaching Assistant (TA) for Jon Claerbout's class I prepared
several lectures on DMO. Two of them appear polished enough
to be included in this report. The first part explains
the DMO correction in simple, geometrical terms and
justifies its place in the imaging processing sequence. The second
part deals with DMO by Fourier methods.
Detecting gravitational waves using seismic data (ps 1636K) (src 7213K)
Abma R.
Several years of seismic data acquired by the international deployment
of accelerometers (IDA) are used in an attempt to detect
gravitational waves radiated from low-frequency astronomical binary sources.
These data were preconditioned with various
combinations of
earthquake removal, gain, and tapering.
Directionally weighted spectra were
calculated for 0.012 to 0.556 milli-Hz (one day to one-half hour periods)
in 84 directions, one year at a time, with correction for the earth's
rotation.
While patterns similar to the synthetic response from a
gravitational-wave source were observed, these patterns showed no
consistency when compared between years. This inconsistency suggests
that the patterns are noise and not the result of gravitational wave
excitation by binary sources.
Analysis of ultrasonic velocities in hydrocarbon mixtures (ps 49K) (src 13K)
Berryman J. G.
Ultrasonic velocity data on hydrocarbon mixtures was shown by
Wang and Nur [JASA 89, 2725 (1991)] to agree quite well with the
predictions of a simple mixing rule (volume average of velocity).
The same data is reanalyzed using Wood's formula and the
time average approximation. Wood's formula for acoustic velocity is
shown to be always less than the time average formula, which is itself always
less than the simple mixing rule result. Although the volume average rule
agrees best with the data on binary mixtures of 1-decene and
1-octadecene, all these formulas agree with the data to within 1%
and, therefore, it is not possible to distinguish among the formulas
using this data set.
Similar results are also found for six multicomponent hydrocarbon mixtures.
The C++ language in physical science (ps 74K) (src 66K)
Nichols D., Dunbar G., and Claerbout J.
We have designed C++ classes that are used to solve optimization
problems involving linear operators. The use of C++ enables us
to write code to solve these problems at a much higher level than when
writing in Fortran. The ability to design classes that abstract the
concepts of operators and spaces enables us to separate the task of writing
new operators from the task of writing routines to solve the optimization
problem.
An implementation of operators and spaces in C++ (ps 70K) (src 152K)
Dunbar G.
This paper is a companion to the previous paper Nichols et al. (1992)
which gives an overview of the problems that these C++ classes are
designed to solve. It is a collection of manual pages describing my
C++ work this summer, with a short extra explanation preceeding each
page. It is intended as a reference document for someone who wants
more details about the code that we have written. It is probably most
useful to a reader who is already familiar with C++.
The manual pages are in an order such that every class or function is
...
Xtpanel: an interactive panel builder (ps 350K) (src 1082K)
Cole S. and Nichols D.
Xtpanel builds interactive panels - containing objects such
as buttons, sliders, and dialog boxes - from a simple script file
or from the command line.
With xtpanel, one can quickly add a layer of interactivity to
existing software.
For instance, a velocity analysis tool can be created in minutes
by using xtpanel to add an interactive front end, where sliders choose
velocities from a user-specified range, to an existing NMO correction
program.
Panels can take advantage not only of existing application programs,
but also the utilities built into the UNIX operating system.
In one example, we use an 80-line script to build an X windows calculator
by making a front end to the line-oriented UNIX calculator
bc. Another utility built with xtpanel is the xtpanel generator.
This is a series of panels that let users build new panels interactively,
without having to learn and use the script language.