

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: LEAKY INTEGRATION
Up: Table of Contents
Z-plane, causality, and feedback
All physical systems share the property that they do not respond
before they are excited.
Thus the impulse response of any physical system
is a one-sided time function (it vanishes before t = 0).
In system theory such a filter function is called ``realizable"
or ``causal.''
In wave propagation this property is associated with causality
in that no wave may begin to arrive before it is transmitted.
The lag-time point t = 0 plays a peculiar and an important role.
Thus many subtle matters can be more clearly understood
with sampled time than with continuous time.
When a filter responds at and after lag time t = 0,
we say the filter is realizable or causal.
The word
``causal" is appropriate in physics, where stress causes
instantaneous strain and vice versa,
but one should return to the less pretentious
words ``realizable" or ``one-sided"
when using filter theory to describe economic or social systems
where simultaneity is different from cause and effect.
The other new concept in this chapter is ``feedback."
Ordinarily a filter produces its output using only past inputs.
A filter using feedback uses also its past outputs.
After digesting the feedback concept, we will look at a wide variety
of filter types, at what they are used for, and at how to implement them.
First a short review:
the Z-transform of an arbitrary,
time-discretized signal xt is defined by
| 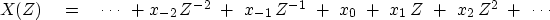 |
(1) |
In chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we saw that (1)
can be understood as a Fourier sum (where
we saw that (1)
can be understood as a Fourier sum (where 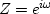 ).
It is not necessary for Z to take on numerical values,
however, in order
for the ideas of convolution and correlation to be useful.
In chapter
).
It is not necessary for Z to take on numerical values,
however, in order
for the ideas of convolution and correlation to be useful.
In chapter
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we defined Z to be the unit delay operator.
Defined thus, Z2 delays two time units.
Expressions like
we defined Z to be the unit delay operator.
Defined thus, Z2 delays two time units.
Expressions like 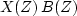 and
and 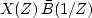 are
useful because they imply convolution and crosscorrelation
of the time-domain coefficients.
Here we will be learning how to interpret 1/A(Z) as a feedback filter,
i.e., as a filter that processes not only past inputs, but past outputs.
We will see that this approach brings with it
interesting opportunities
as well as subtle pitfalls.
are
useful because they imply convolution and crosscorrelation
of the time-domain coefficients.
Here we will be learning how to interpret 1/A(Z) as a feedback filter,
i.e., as a filter that processes not only past inputs, but past outputs.
We will see that this approach brings with it
interesting opportunities
as well as subtle pitfalls.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: LEAKY INTEGRATION
Up: Table of Contents
Stanford Exploration Project
10/21/1998
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we saw that (1)
can be understood as a Fourier sum (where
we saw that (1)
can be understood as a Fourier sum (where ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) we defined Z to be the unit delay operator.
Defined thus, Z2 delays two time units.
Expressions like
we defined Z to be the unit delay operator.
Defined thus, Z2 delays two time units.
Expressions like ![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)