




Next: Two poles
Up: LEAKY INTEGRATION
Previous: LEAKY INTEGRATION
A pole is a place in the complex plane
where a filter B(Zp) becomes infinity.
This occurs where a denominator vanishes.
For example, in equation (8) we see that there is one pole
and it is located at 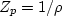 .In plots like Figure 1,
a pole location is denoted by a ``p'' and a zero location by a ``z."
I chose to display the pole and zero locations
in the
.In plots like Figure 1,
a pole location is denoted by a ``p'' and a zero location by a ``z."
I chose to display the pole and zero locations
in the 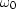 -plane instead of in the Z0-plane.
Thus real frequencies run along the horizontal axis
instead of around the circle of |Z|=1.
I further chose to superpose the complex
-plane instead of in the Z0-plane.
Thus real frequencies run along the horizontal axis
instead of around the circle of |Z|=1.
I further chose to superpose the complex 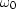 -plane
on the graph of
-plane
on the graph of 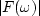 versus
versus  .This enables us to correlate the pole and zero locations to the spectrum.
I plotted
.This enables us to correlate the pole and zero locations to the spectrum.
I plotted 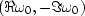 in order that
the
in order that
the  and
and 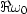 axes would coincide.
As we will see later, some poles give stable filters and some poles
give unstable filters.
At the risk of some confusion, I introduced the minus sign
to put the stable poles atop the positive spectrum.
Since we will never see a negative spectrum and we will rarely see
an unstable pole, this economizes on paper
(or maximizes resolution for a fixed amount of paper).
axes would coincide.
As we will see later, some poles give stable filters and some poles
give unstable filters.
At the risk of some confusion, I introduced the minus sign
to put the stable poles atop the positive spectrum.
Since we will never see a negative spectrum and we will rarely see
an unstable pole, this economizes on paper
(or maximizes resolution for a fixed amount of paper).
In Figure 1,
moving the ``p'' down toward the horizontal axis would cause
a slower time decay and a sharper frequency function.





Next: Two poles
Up: LEAKY INTEGRATION
Previous: LEAKY INTEGRATION
Stanford Exploration Project
10/21/1998