




Next: The accuracy of causal
Up: Z-plane, causality, and feedback
Previous: Smoothing with a triangle
Begin with a function in discretized time xt.
The Fourier transform with the substitution 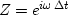 is
the Z-transform
is
the Z-transform
| 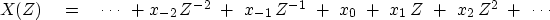 |
(12) |
Define 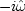 (which will turn out to be an approximation
to
(which will turn out to be an approximation
to 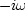 ) by
) by
| 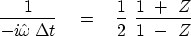 |
(13) |
Define another signal yt
with Z-transform Y(Z) by
applying the operator to X(Z):
| 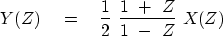 |
(14) |
Multiply both sides by (1-Z):
| 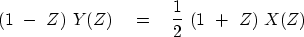 |
(15) |
Equate the coefficient of Zt on each side:
| 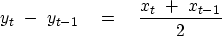 |
(16) |
Taking xt to be an impulse function,
we see that yt turns out
to be a step function, that is,
| 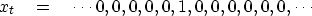 |
(17) |
| 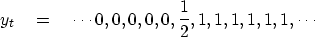 |
(18) |
So yt is the discrete-domain representation of the integral
of xt from minus infinity to time t.
The operator (1+Z)/(1-Z) is called the
``bilinear transform."





Next: The accuracy of causal
Up: Z-plane, causality, and feedback
Previous: Smoothing with a triangle
Stanford Exploration Project
10/21/1998
![]() is
the Z-transform
is
the Z-transform