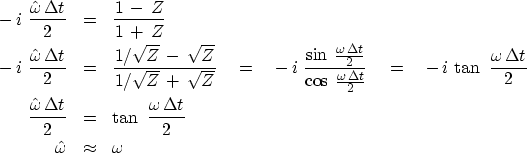Next: Examples of causal integration
Up: CAUSAL INTEGRATION FILTER
Previous: CAUSAL INTEGRATION FILTER
The accuracy of the approximation of 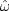 to
to  can be seen by dividing the top and bottom of equation (13)
by
can be seen by dividing the top and bottom of equation (13)
by 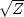 and substituting
and substituting 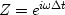 :
:
| 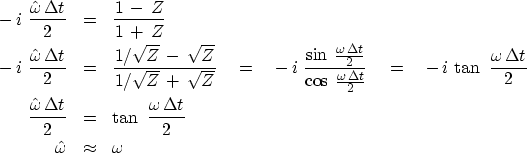 |
(19) |
| (20) |
| (21) |
| (22) |
This is a valid approximation at low frequencies.





Next: Examples of causal integration
Up: CAUSAL INTEGRATION FILTER
Previous: CAUSAL INTEGRATION FILTER
Stanford Exploration Project
10/21/1998
![]() to
to ![]() can be seen by dividing the top and bottom of equation (13)
by
can be seen by dividing the top and bottom of equation (13)
by ![]() and substituting
and substituting ![]() :
: