




Next: DAMPED OSCILLATION
Up: CAUSAL INTEGRATION FILTER
Previous: Symmetrical double integral
Integration can be thought of as 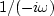 .The implied division by zero at
.The implied division by zero at 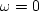 warns us that
this filter is not quite normal.
For example,
warns us that
this filter is not quite normal.
For example, 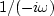 appears to be an imaginary, antisymmetric function of
appears to be an imaginary, antisymmetric function of  .This implies that the time function
is the real antisymmetric signum function,
namely,
.This implies that the time function
is the real antisymmetric signum function,
namely, 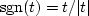 .The signum is not usually thought of as an integration operator,
but by adding a constant we have a step function,
and that is causal integration.
By subtracting a constant we have anticausal integration.
We can play games with the constant
because it is at zero frequency
that the definition contains zero division.
.The signum is not usually thought of as an integration operator,
but by adding a constant we have a step function,
and that is causal integration.
By subtracting a constant we have anticausal integration.
We can play games with the constant
because it is at zero frequency
that the definition contains zero division.
EXERCISES:
-
Show that the mean of the input of leaky()
is the mean of the output,
which demonstrates that the gain of the filter is unity at zero frequency.





Next: DAMPED OSCILLATION
Up: CAUSAL INTEGRATION FILTER
Previous: Symmetrical double integral
Stanford Exploration Project
10/21/1998