It seems we can represent a sinusoid by Z-transforms
by setting a pole on the unit circle.
Taking ![]() , we have the filter
, we have the filter
| |
(25) |
Now, how can we make a real-valued sinusoid starting at t=0?
Just as with zeros, we need to complement the pole at ![]() by one at
by one at ![]() .The resulting
signal bt is shown on the left in Figure 7.
On the right is a graphical attempt to plot the impulse function
of dividing by zero at
.The resulting
signal bt is shown on the left in Figure 7.
On the right is a graphical attempt to plot the impulse function
of dividing by zero at ![]() .
.
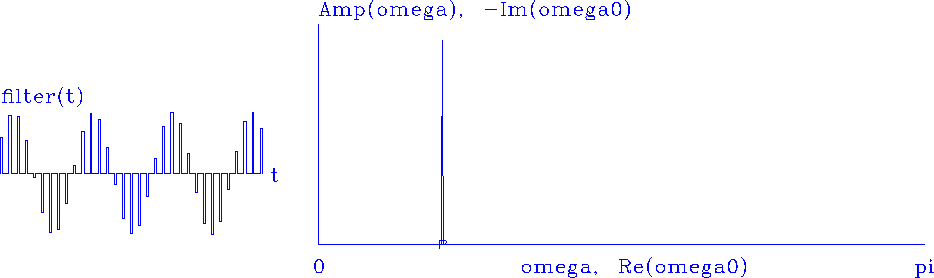 |
Next, let us look at a damped case like leaky integration.
Let ![]() and
and ![]() .Then
.Then ![]() .Define
.Define
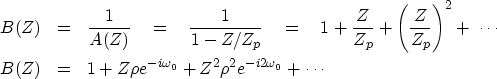 |
(26) | |
| (27) |
| (28) |
The wavelet bt is complex.
To have a real-valued time signal,
we need another pole at the negative frequency,
say ![]() .So the composite denominator is
.So the composite denominator is
| |
(29) |
Multiplying the two poles together as we did for roots results in the plots of 1/A(Z) in Figure 8.
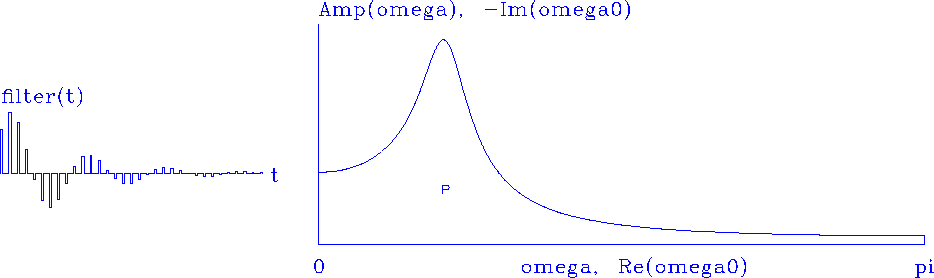 |
Notice the ``p'' in the figure.
It indicates the location of the pole Zp
but is shown in the ![]() -plane,
where
-plane,
where ![]() .Pushing the ``p'' left and right will lower and raise the resonant frequency.
Pushing it down and up will raise and lower the duration of the resonance.
.Pushing the ``p'' left and right will lower and raise the resonant frequency.
Pushing it down and up will raise and lower the duration of the resonance.