 |
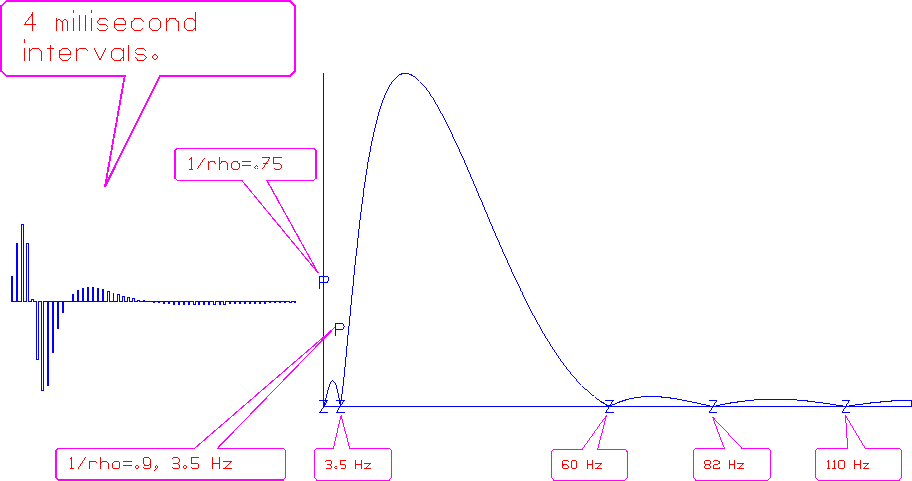
Figure 17 My favorite wavelet for seismic modeling.
 |
I use some zeros at high frequency to force continuity in the time domain and a zero at the origin to suppress zero frequency. I like to simulate the suppression of low-frequency ground roll, so I put another zero not at the origin, but at a low frequency. Theory demands a conjugate pair for this zero; effectively, then, there are three roots that suppress low frequencies. I use some poles to skew the passband toward low frequencies. These poles also remove some of the oscillation caused by the three zeros. (Each zero is like a derivative and causes another lobe in the wavelet.) There is a trade-off between having a long low-frequency tail and having a rapid spectral rise just above the ground roll. The trade-off is adjustable by repositioning the lower pole. The time-domain wavelet shows its high frequencies first and its low frequencies only later. I like this wavelet better than the Ricker wavelet (second derivative of a Gaussian). My wavelet does not introduce as much signal delay. It looks like an impulse response from the physical world.