

![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Angle-Domain Common Image Gathers
Up: Table of Contents
3-D Angle-domain common-image gathers for migration velocity analysis
Biondo Biondi and Thomas Tisserant
biondo@sep.stanford.edu
Wavefield-continuation migration methods have the potential
of producing high-quality images even
when complex overburden severely distorts the wavefield.
However, as for all migration methods, the quality
of the final image is strongly dependent on the accuracy
of the velocity model.
In complex area the velocity model is usually estimated in
an iterative process called Migration Velocity Analysis (MVA).
At each iteration of an MVA process the velocity is updated based
on the information extracted from the current migrated image,
and, in particular, from the Common Image Gathers (CIGs).
The computation of accurate CIG is thus crucial for any MVA
method.
Most of the current MVA methods for wavefield-continuation
migration
employ Angle-Domain CIGs (ADCIGs)
Biondi and Sava (1999); Clapp and Biondi (2000); Liu et al. (2001); Mosher et al. (2001).
The computation of ADCIGs with wavefield-continuation migration
is based on a plane-waves
decomposition of the wavefield either before imaging
Mosher et al. (1997); Prucha et al. (1999); Xie and Wu (2002); de Bruin et al. (1990),
or after imaging Biondi and Shan (2002); Rickett and Sava (2002); Sava and Fomel (2003).
The methods previously presented in the literature are limited
to the computation of 2-D ADCIGs that are functions of the
aperture angle 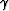 only.
These methods have been applied to 3-D marine data
by assuming zero-azimuth reflections;
this assumption is approximately correct for marine data that
have been acquired with a narrow-azimuth acquisition geometry.
only.
These methods have been applied to 3-D marine data
by assuming zero-azimuth reflections;
this assumption is approximately correct for marine data that
have been acquired with a narrow-azimuth acquisition geometry.
In this paper we present the computation
and the geometric interpretation of full 3-D ADCIGs
that decompose the image not only according to the
aperture angle 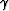 , but also to
the reflection azimuth
, but also to
the reflection azimuth 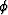 .We extend to 3-D both methods for computing ADCIGs:
before and after imaging.
Our analysis shows that the 2-D equation that relates
the in-line offset ray parameter pxh
to the aperture angle
.We extend to 3-D both methods for computing ADCIGs:
before and after imaging.
Our analysis shows that the 2-D equation that relates
the in-line offset ray parameter pxh
to the aperture angle 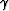 is also valid in 3-D for zero-azimuth reflections,
when used in combination with common-azimuth migration
Biondi and Palacharla (1996).
This result supports the previous use
of 2-D ADCIGs computed before imaging
for MVA of 3-D marine data
Biondi and Vaillant (2000); Clapp (2001); Liu et al. (2001); Mosher et al. (2001).
In contrast, the 2-D transformation to angle domain
performed after imaging
Sava and Fomel (2003)
is not correct in 3-D,
not even in the case of zero-azimuth reflections;
its use in presence of cross-line dips
leads to the overestimation of the
reflection-aperture angle
is also valid in 3-D for zero-azimuth reflections,
when used in combination with common-azimuth migration
Biondi and Palacharla (1996).
This result supports the previous use
of 2-D ADCIGs computed before imaging
for MVA of 3-D marine data
Biondi and Vaillant (2000); Clapp (2001); Liu et al. (2001); Mosher et al. (2001).
In contrast, the 2-D transformation to angle domain
performed after imaging
Sava and Fomel (2003)
is not correct in 3-D,
not even in the case of zero-azimuth reflections;
its use in presence of cross-line dips
leads to the overestimation of the
reflection-aperture angle 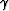 .
In either case (before or after imaging),
when the azimuth of the reflections
is not oriented along the in-line direction,
we must use the full 3-D methodology to
obtain accurate ADCIGs.
.
In either case (before or after imaging),
when the azimuth of the reflections
is not oriented along the in-line direction,
we must use the full 3-D methodology to
obtain accurate ADCIGs.
The geometrical understanding we developed
when generalizing 2-D ADCIGs to 3-D ADCIGs
enables us to generalize the analysis of the kinematics
of 2-D ADCIGs in the presence of migration-velocity errors
that was presented by
Biondi and Symes (2003).
However their purely ray-theoretical analysis of 2-D ADCIGs cannot
be directly extended because in 3-D the source and receiver rays
are not guaranteed to be coplanar.
Fortunately, a plane-wave interpretation
of 3-D ADCIGs overcomes these difficulties
because the two plane waves corresponding to the source and receiver rays
define a plane of coplanarity that passes through the angle-domain image point.
Once this plane is defined,
the 2-D kinematic analysis
carries over to 3-D and we can define a quantitative
relationship between the reflectors' movement along the apparent
geological dip and the traveltime perturbations caused
by velocity errors.
This relationship can be directly used in a tomographic inversion
of 3-D ADCIGs;
we use it to define a 3-D RMO function
for measuring kinematic errors from 3-D ADCIGs.
ADCIGs have been introduced also for integral
migration methods
(e.g. Kirchhoff and Generalized Radon Transform);
Xu et al. (2001) defined and applied them in 2-D,
Brandsberg-Dahl et al. (2003)
defined them in 3-D and applied them in 2.5-D,
and Brandsberg-Dahl et al. (1999) applied 2-D ADCIGs
to MVA.
ADCIGs computed by Kirchhoff-like migration
share many properties with ADCIGs
computed by wavefield-continuation migration.
However, in complex media,
the two types of ADCIG have subtle kinematic differences,
as clearly demonstrated by Stolk and Symes (2004).
A thorough comparison of these two types of ADCIG
would be of theoretical and practical value,
but we consider it beyond the scope of this paper.


![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)


Next: Angle-Domain Common Image Gathers
Up: Table of Contents
Stanford Exploration Project
5/23/2004
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)