Angle-Domain Common Image Gathers before imaging

This paper presents two methods for computing 3-D ADCIGs in conjunction with wavefield-continuation migration. Both methods rely on a decomposition of the wavefield into plane-wave components; this decomposition is performed by slant stacks Schultz and Claerbout (1978) along the subsurface offset axes. The two methods differ in the stage of the migration process during which the plane-wave decomposition is performed (before imaging or after imaging), but in both cases the plane-wave decomposition links the ray-theoretical and the plane-wave interpretation of ADCIGs that we use in this paper. We equate the propagation direction of plane waves with the propagation direction of specular rays, and thus we implicitly make a stationary-phase approximation that assumes that the seismic events are not dispersive; that is, that wavefronts are locally planar and coherent for all frequencies. This assumption is not strictly necessary because our analysis is valid for each frequency component, but nonetheless we believe that the advantages in simplicity are worthwhile the apparent loss of generality.

We start by presenting the method based on an angle decomposition before imaging Prucha et al. (1999); de Bruin et al. (1990) because it has the most direct physical interpretation. The physical interpretation of the ADCIGs computed after imaging Biondi and Shan (2002); Rickett and Sava (2002); Sava and Fomel (2003) follows directly from the interpretation of the ADCIGs computed before imaging.

A 3-D prestack data set can be decomposed according to the offset ray parameters (p_xh,p_yh) by applying slant stacks along the offset axes. These slant stacks produce plane-wave components called offset plane waves. If the velocity function is horizontally invariant, each offset plane wave can be accurately propagated and imaged independently from the others. Each prestack partial image produced by this procedure corresponds to one offset ray parameter, and thus ADCIG functions of the offset ray parameters [ADCIG$\left(p_{x_h},p_{y_h}\right)$]can be extracted from the whole prestack image cube. The offset ray parameters measured at the surface are functions of the surface take-off angles of the source and receiver rays, and are obviously linked with the reflection opening angle $\gamma$and the reflection azimuth $\phi$.

Ottolini and Claerbout (1984) presented a procedure for obtaining angle-dependent images based on the slant-stack of 2-D CMP gathers at the surface and on the propagation of offset plane waves. Mosher et al. (1997) generalized the 2-D procedure to 3-D marine data and derived a more accurate downward-continuation method for the offset plane waves. However, there is a limit on the accuracy of a migration based on an offset plane-wave decomposition at the surface. When the velocity function is laterally varying, the source and receiver wavefields are refracted differently, according to the local velocities. Consequently, the independent propagation of each offset plane wave is inaccurate when strong lateral velocity variations occur. In these situations, the idea of decomposing the wavefield into offset plane waves is still useful, but it must be generalized; the prestack wavefield must be slant-stacked recurrently at each depth level, instead of only once at the surface.

When source-receiver migration (i.e. survey sinking) is applied, the whole prestack wavefield is obtained at every depth level as the result of recursively downward continuing the recorded data using the Double Square Root (DSR) operator Claerbout (1985). Therefore, once we have introduced the concept of decomposing the prestack wavefield at depth, the derivation of the procedure for computing ADCIGs before imaging using source-receiver downward continuation is straightforward Prucha et al. (1999).

In conventional source-receiver migration the image is then obtained by extracting the values of the wavefield at zero time (t=0). The migration process can be schematically represented as follows:

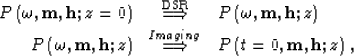$$\begin{eqnarray} \P\left(\omega,{\bf m},{\bf h};z=0\right) & \stackrel{{\rm DSR}... ...{Imaging}{\Longrightarrow} & \P\left(t=0,{\bf m},{\bf h};z\right),\end{eqnarray}$$ (1) (2)

where $P\left(\omega,{\bf m},{\bf h};z\right)$is the wavefield at the temporal frequency $\omega$,the midpoint ${\bf m}$, the offset ${\bf h}$, and at depth z.

To compute ADCIGs, we need to introduce a slant-stack transformation between downward continuation [step (1)] and imaging [step (2)]. The results of slant stacks are functions of the offset ray parameter ${\bf {p_{h}}}$and the intercept time $\tau$.The image is then obtained by extracting the values of the wavefield at zero intercept time; i.e. $\tau=0$.The migration process used to produce ADCIGs can be schematically represented as follows:

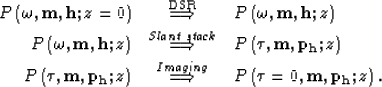$$\begin{eqnarray} \P\left(\omega,{\bf m},{\bf h};z=0\right) & \stackrel{{\rm DSR}... ...{\Longrightarrow} & \P\left(\tau=0,{\bf m},{\bf {p_{h}}};z\right).\end{eqnarray}$$ (3) (4) (5)

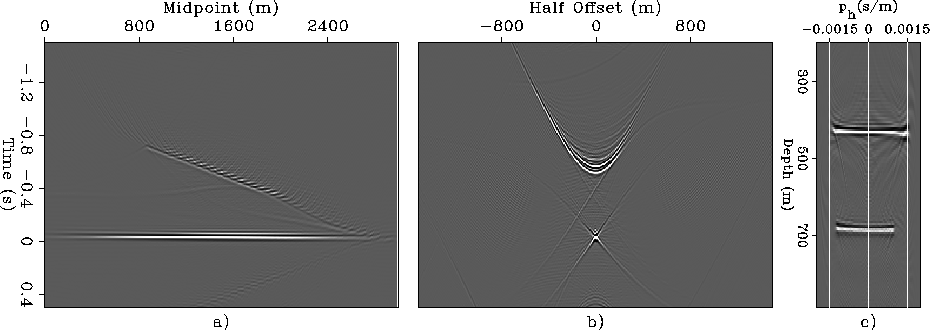
Figure 1 illustrates the subsequent stages of the process represented in (3-5). The synthetic data set imaged to create this figure was modeled assuming two reflectors (one dipping and one flat) immersed in a constant-velocity medium. The downward-continuation process [step (1) or step (3)] focuses the wavefield toward zero offset; if the continuation velocity is correct, a migrated image can be obtained by extracting the value of the wavefield at zero offset and zero time. Figure 1a shows the zero-offset section of the downward-continued wavefield at the depth of the flat reflectors; that is, at z=700 meters. As expected, the flat reflector is well imaged at zero time. Figure 1b shows the wavefield at the same depth as in Figure 1a, but as a function of offset and at fixed midpoint (x_m=1,410 meters). The flat reflector is well focused at zero offset and zero time, whereas the energy corresponding to the dipping reflector has already been defocused and thus it appears as a ``time-reversed'' hyperbola at negative times. The wavefield shown in Figure 1b is decomposed into plane waves by performing slant stacks for each midpoint location [step (4)], and the results of these slant stacks are imaged at zero time [step (5)]. The downward-continuation, slant stacks, and imaging steps are repeated for all depth levels. Figure 1c shows the ADCIG at x_m=1,410 meters, for all depths. Both reflectors are imaged as flat events in the ADCIGs, because at each depth, slant stacks transform band-limited impulses located at zero offset (like the one shown in Figure 1b) into flat events.

 

zoff-cmp-cig-dip-overn-z700
Figure 1 Illustration of the method for computing ADCIGs before imaging. Orthogonal slices of the prestack wavefield after downward continuation with the correct velocity to the depth of 700 meters; that is, the depth of the flat reflector: zero-offset section (panel a), and the common-midpoint gather at 1,410 meters (panel b). Panel c) shows the complete (i.e. for all depths) ADCIG at 1,410 meters.

Computing ADCIGs before imaging is more difficult when using shot-profile migration than when using source-receiver migration, because the prestack wavefield at depth is not easily available as a function of the subsurface offset. In theory, it could be computed by appropriate correlations (or deconvolutions) of the source and receiver wavefields de Bruin (1992). This procedure generates ADCIGs equivalent to those obtained by source-receiver migration, as it can be demonstrated by a generalization of the equivalence principle for the prestack images demonstrated by Wapenaar and Berkhout (1987) and Biondi (2003). The computation of the ADCIGs before imaging for shot-profile migration is computationally demanding, because it requires either decomposing the wavefield for each shot independently and accumulating the prestack images for all shots (computationally inefficient), or, accumulating the contributions of each shot to the whole prestack wavefield before decomposing it (storage and I/O inefficient). Therefore, ADCIGs are rarely computed before imaging when using shot-profile migration. In the next section we will see how computing ADCIGs after imaging addresses this problem.

 

• Geometric interpretation of 3-D ADCIG$\left(p_{x_h},p_{y_h}\right)$