Examples of 3-D ADCIGs

This section presents several examples of 3-D ADCIGs. The first example is taken from the SEG-EAGE salt data set Aminzadeh et al. (1996). It illustrates the error introduced when the approximate 2-D relationship [equation (16)] is used instead of the correct 3-D one [equation (17)] to estimate the aperture angle $\gamma$in presence of significant geological dips.

Figure 5 shows a depth slice (z=580 meters) of the migrated image of the SEG-EAGE salt data set. The crosshair is centered at a horizontal location where the top of the salt dips at approximately 50 degrees in the cross-line direction and is flat along the in-line direction. Figure 6 shows the ADCIGs computed at the location marked by the crosshair. Figure 6a was computed using the 2-D relationship [equation (16)], whereas Figure 6b was computed using the 3-D relationship [equation (17)]. The aperture angle is overestimated in the gather on the left (apparent maximum aperture is about 60 degrees), and correctly estimated in the gather on the right (apparent maximum aperture is about 48 degrees). This error is consistent with the factor $\cos\alpha_y{'}$ that is neglected in the 2-D case. Notice that the bottom of the salt reflection ($z\simeq$ 2,100 meters) is unchanged, because it is flat.

 

comp-2d-vs-3d-depth-slice Figure 5 Depth slice (z=580 meters) of the migrated image of the SEG-EAGE salt data set. The crosshair is centered at a horizontal location where the top of the salt dips at approximately 50 degrees in the cross-line direction.

 

comp-2d-vs-3d-adcigs Figure 6 ADCIG computed using the approximate 2-D relationship (panel a), and ADCIG computed using the correct 3-D relationship (panel b). The aperture angle 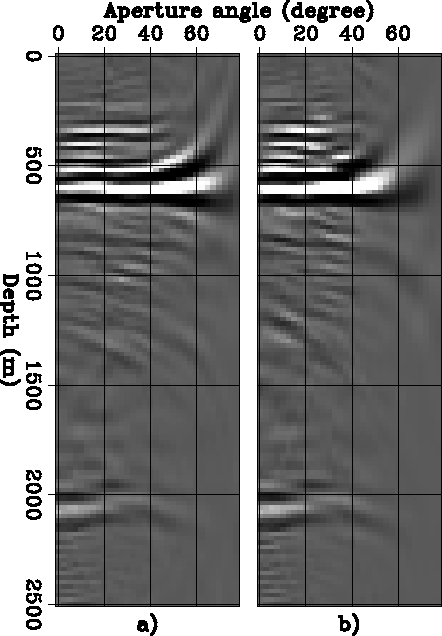$\gamma$of the top of the salt reflection ($z\simeq$ 600 meters) is overestimated in panel (a), whereas the bottom of the salt reflection ($z\simeq$ 2,100 meters) is the same in the two panels.

In 3-D, ADCIGs are five-dimensional objects, and thus it can be challenging to gain an intuitive understanding of their behavior. The next set of figures shows 2-D slices of the 5-D space generated by computing 3-D ADCIGs from the migrated cube obtained from a simple synthetic data set. The data set contains 5 dipping planes, dipping at $0^\circ$, $15^\circ$, $30^\circ$, $45^\circ$ and $60^\circ$ toward increasing x and y. The azimuth of the planes is 45 degrees with respect to the direction of the acquisition. The velocity is $V\left(z\right)= \left(1,500 + .5 z\right)$ m/s, which roughly corresponds to typical gradients found in the Gulf of Mexico. The acquisition geometry had a single azimuth oriented along the x axis, and the maximum source-receiver offset was 3,000 meters. Figure 7 shows the geometry of the reflectors. The data were imaged with a full source-receiver 3-D prestack migration.

Because of the velocity gradient and the oblique azimuthal orientation, the azimuths of the reflections are not equal to the azimuth of the acquisition ($\phi=0$). The reflection azimuths are within the range of $0^\circ\leq \phi\leq 15^\circ$and depend on the reflector dip and on the aperture angle $\gamma$.The steeper the reflector dip and the wider the aperture angle are, the larger the azimuth rotation is at the reflection point.

All the following figures show slices of the ADCIGs at one fixed horizontal location with x=y=450 meters; that is, they show slices through the 3-D image cube described as ADCIG$\left(z,\gamma,\phi\right)$.The most familiar of these slices display the image as a function of the depth (z) and the aperture angle ($\gamma$). Figure 8 shows two of these ADCIGs, for two different reflection azimuths: $\phi=10$ degrees (panel a) and $\phi=15$ degrees (panel b). The reflections from the deepest - and steepest - reflector ($z\simeq$ 1,430 meters) are well focused within the range delimited by these two azimuths. In contrast, the reflections from the other two reflectors (dipping at 30 and 45 degrees), are not well focused at these azimuths, and thus they frown downward even if the migration velocity is correct.

Figure 9 shows a slice taken at the constant depth of z=1,430 meters; this depth corresponds to the deepest reflector. The reflection amplitudes are thus shown as functions of both the aperture angle ($\gamma$) and the reflection azimuth ($\phi$). Because of the poor azimuthal resolution close to normal incidence, the azimuthal range is wide for small $\gamma$;it narrows around $\phi=15$ degrees as $\gamma$ increases.

The increasing azimuthal resolution with aperture angle is clearly demonstrated in Figure 10. The three panels in Figure 10 display the image as a function of depth (z) and reflection azimuth ($\phi$), and at constant aperture angle. The aperture angles are: a) $\gamma$=4 degrees, b) $\gamma$=20 degrees, and c) $\gamma$=30 degrees. The curvature of the reflectors as a function of the azimuth increases with increasing aperture angle, indicating that the azimuthal resolution increases as the aperture angle widens. In other words, the common-azimuth data ``illuminates'' all the reflection azimuths for narrow aperture angles, but ``illuminates'' only a narrow range of reflection azimuths at wide aperture angles.

 

planes Figure 7 Reflectors' geometry for the synthetic data set used to illustrated 3-D ADCIGs. The reflectors are slanted planes, dipping at 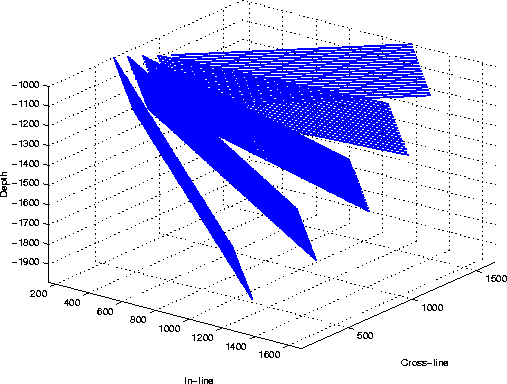$0^\circ$, $15^\circ$, $30^\circ$, $45^\circ$ and $60^\circ$ toward increasing x and y; they are oriented with an azimuth of $45^\circ$ with respect to the in-line direction.

 

cig-1-data8 Figure 8 ADCIGs as functions of depth (z) and aperture angle (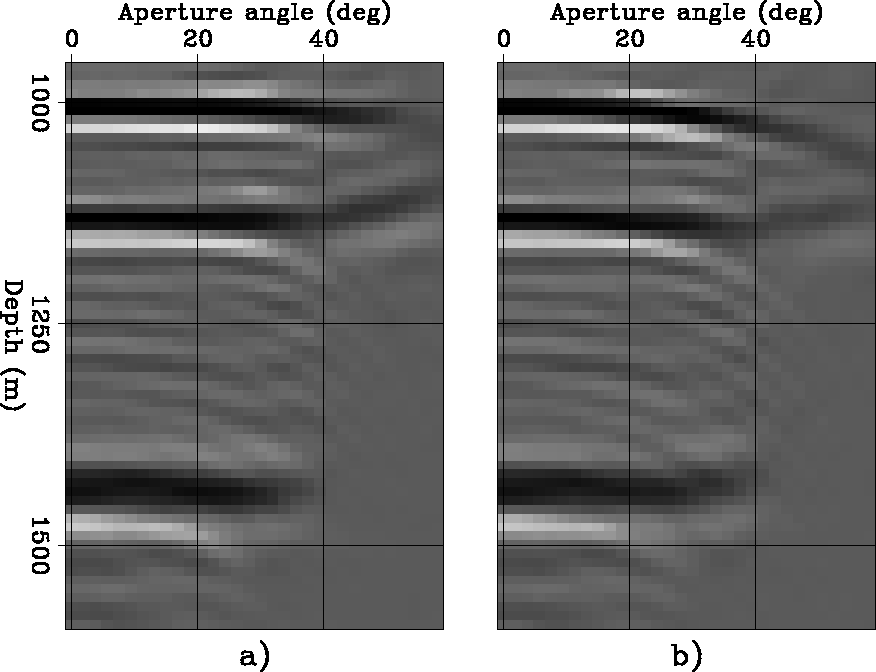$\gamma$) for two different reflection azimuths and at constant horizontal location (x=y=450 meters): $\phi=10^\circ$ (a), and $\phi=15^\circ$ (b).

 

zaz-60-60-dense-all-v4-data8 Figure 9 ADCIG as a function of aperture angle ($\gamma$)and reflection azimuth ($\phi$)at constant depth (z=1,430 meters) and horizontal location (x=y=450 meters).

 

azim-gamma-all-data8 Figure 10 ADCIGs as functions of depth (z) and reflection azimuth (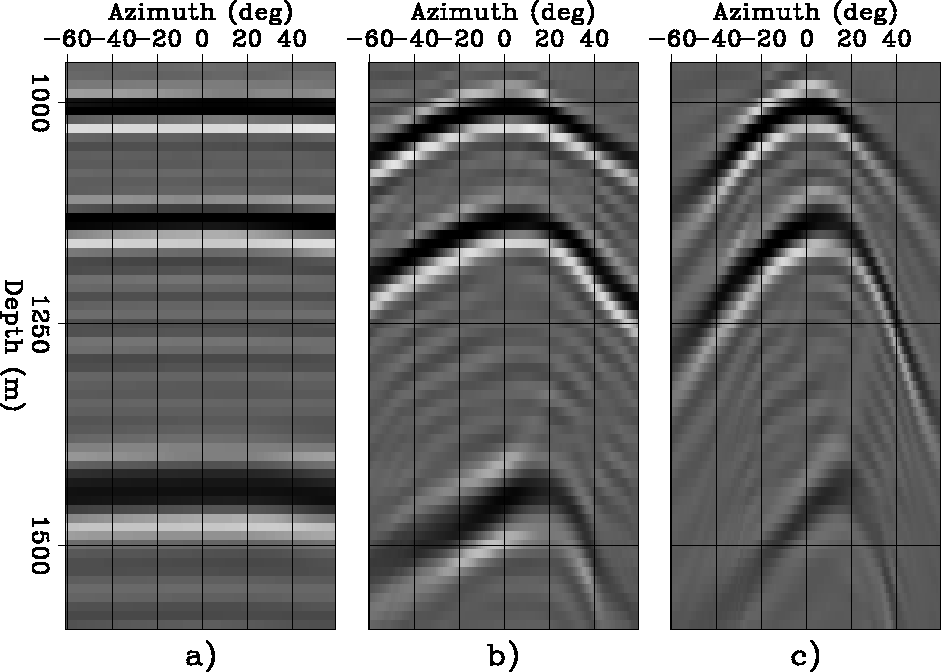$\phi$)for three different aperture angles and at constant horizontal location (x=y=450 meters): $\gamma=4^\circ$ (a), $\gamma=20^\circ$ (b), and $\gamma=30^\circ$ (c).