Angle-Domain Common Image Gathers after imaging - ADCIG$\left(\gamma,\phi\right)$

 The computation of ADCIGs before imaging has a straightforward physical interpretation, and thus it was the first methodology to be developed for both and shot-profile migration de Bruin et al. (1990) and source-receiver migration Prucha et al. (1999). However, as we have discussed in the previous section, the computation of ADCIGs before imaging with shot-profile migration can be either computationally or I/O demanding. Sava and Fomel (2003) recognized that for source-receiver migration, the plane-wave decomposition can be performed after applying the imaging condition, as well as before. Rickett and Sava (2002) applied this insight to compute 2-D ADCIGs after shot-profile downward continuation. Their method is based on the generalization of the conventional imaging condition for shot-profile migration that we summarize in the next paragraph. When using this imaging condition we compute a prestack image function of the subsurface half offset ${\bf h}$,as well as of depth z and the midpoint ${\bf m}$.

If $P^s_{z}\left(\omega,x,y;{\bf s}_{i}\right)$and $P^g_{z}\left(\omega,x,y;{\bf s}_{i}\right)$are respectively the source wavefield and the recorded wavefield downward-continued to depth z for the i-th source location ${\bf s}_{i}$,as functions of the subsurface horizontal coordinates $\left(x,y\right)$,the image is formed by first cross-correlating the two wavefields along the time axis (multiplication by the complex conjugate in the frequency domain) and then evaluating the correlation at zero time (summation over frequencies) as following:  

$${I\left({\bf m},{\bf h};z\right)} = \sum_{i} \sum_{\omega} ... ...ine { P^s_{z}\left(\omega,x-{x_h},y-{y_h};{\bf s}_{i}\right) }.$$ (13)

The physical interpretation of the subsurface offsets from equation (13) is not immediate. However, it can be demonstrated Biondi (2003); Wapenaar and Berkhout (1987) that the prestack image $I\left({\bf m},{\bf h};z\right)$obtained by equation (13) is equivalent to the image obtained by source-receiver migration applying the procedure outlined in equations (1) and (2). The subsurface offsets can thus be equated to the data offset of the recorded data datumed at depth.

The computation of the ADCIGs after imaging is based on a plane-wave decomposition of the prestack image $I\left({\bf m},{\bf h};z\right)$ - which is obtained by either source-receiver migration or shot-profile migration - by applying slant-stacks along the offset axes, similarly to the computation before imaging that we discussed in the previous section. The only difference between the two methods (before and after imaging) is that the dips along the offset axes are affected by the transformation from time to depth that is implicit in the imaging step. Therefore, the offset-dip parameters are linked to the reflection opening angle $\gamma$and azimuth $\phi$ differently than in the previous case. We will now derive and discuss the analytical relationships between reflection angles and offset dips after imaging. We will start with the simpler 2-D case Sava and Fomel (2003), and then address the general 3-D case Biondi et al. (2003).

The application of the imaging condition transforms a wavefield propagating in time into an image cube that is a function of depth. The transformation from time to depth depends on the local dips in the wavefield and the local propagation velocity. In the frequency-wavenumber domain this transformation is represented by the DSR operator, which in 2-D can be expressed as a function of the angles $\beta_s$ and $\beta_r$as follows:  

$$k_z=-\frac{\omega}{v\left(z,x\right)} \left(\cos \beta_r+ \cos \beta_s\right).$$ (14)

Recalling the relationship between the in-line offset wavenumber k_xh and the in-line offset ray parameter p_xh:  

$$k_{x_h}=p_{x_h}\omega,$$ (15)

and substituting both equation (14) and equation (9) in equation (15), we obtain the following relationship:  

$$k_{x_h} = -p_{x_h}\frac{k_zv\left(z,x\right)}{\cos \beta_r+ ... ...\left(z,x\right)}{2\cos \gamma\cos \alpha_x} = -k_z\tan \gamma.$$ (16)

This relationship directly links the dips in the depth-offset domain $\left(k_{x_h}/k_z\right)$to the aperture angle $\left(\tan \gamma\right)$.

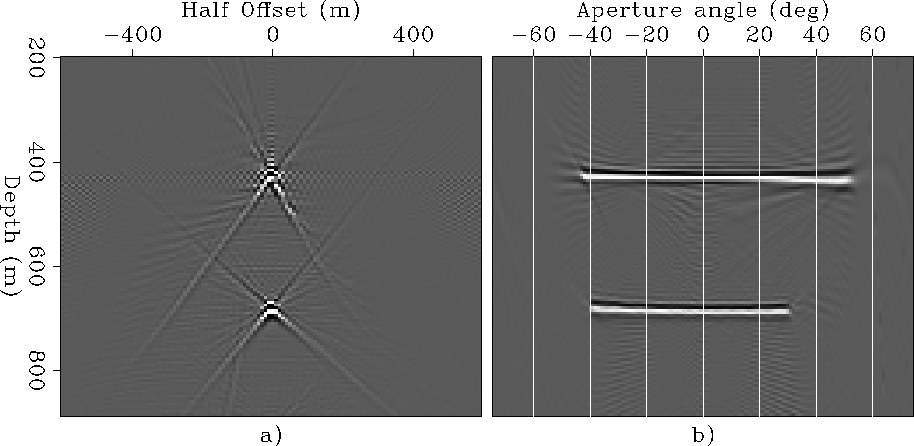
Figure 4 illustrates the computation of 2-D ADCIGs after imaging with a synthetic example. It is analogous to Figure 1, which illustrates the computation of 2-D ADCIGs before imaging. Figure 4a shows a vertical section of the prestack image taken at constant midpoint. We will refer to this kind of section as an Offset Domain Common Image Gather (ODCIG). This ODCIG was obtained with the correct velocity, and the energy is well focused at zero offset for both the dipping and the flat reflectors. Slant stacks transform the impulses at zero offset into flat events in the angle domain (Figure 4b).

 

off-ang-cig-dip-overn-dz5
Figure 4 ODCIG (panel a) and ADCIG$\left(\gamma\right)$ (panel b) after migration with the correct velocity. This CIGs are taken from the same data and at the same surface location as the ADCIG shown in Figure 1c.

To generalize the 2-D offset-to-angle transformation to 3-D, we use the coplanarity condition and the geometrical model shown in Figure 3. In this context, the 2-D DSR expressed in equation (14) describes upward-propagating waves on the tilted plane shown in Figure 3, instead of the vertical plane shown in Figure 2. Consequently, the vertical wavenumber in equation (14) is now the vertical wavenumber along the tilted vertical axis k_z', and not the vertical wavenumber along the ``true'' vertical direction. This distinction is irrelevant in the case of ADCIGs computed before imaging because the computation is performed at each depth level independently, but it is required in this case because the plane-wave decomposition is performed in the depth domain.

If $\delta_{s'}$ and $\delta_{r'}$ are the angles that the source and receiver rays (plane waves) form with the ``true'' vertical direction (as indicated in Figure 3), simple trigonometry relates these angles to $\beta_{s'}$ and $\beta_{r'}$ through the tilt angle $\alpha_y{'}$ as follows: $\cos \delta_{s'}=\cos\beta_{s'}\cos\alpha_y{'}$,and $\cos \delta_{r'}=\cos\beta_{r'}\cos\alpha_y{'}$.The vertical wavenumber k_z' is thus related to the vertical wavenumber k_z as follows: $k_z{'}=k_z\cos\alpha_y{'}=\sqrt{k_z^2+k_{y{'}}^2}$.Substituting this relationship into equation (16) leads to its 3-D equivalent:  

$$k_{x{'}_h} = -k_z{'}\tan \gamma = -\sqrt{k_z^2 + k_{y{'}}^2} \tan \gamma.$$ (17)

This 3-D expression is not independent of the geological dips as was its 2-D equivalent [equation (16)]. In the presence of significant cross-line dips, it is thus important to use the correct 3-D expression in place of the approximate 2-D one. Figures 5-6 illustrate with a data example the effects of the cross-line dip correction in equation (17).

When deriving the after-imaging equivalent of equation (11), we need to take into account that $\alpha_x{'}$is also measured along the tilted axis and thus that $\tan \alpha_x{'}= -k_{x{'}}/k_z{'}$.Using equation (11) and equation (17) we derive the following relationship, which expresses k_y'h as a function of the other wavenumbers in the image:  

$$k_{y{'}_h} = -k_{y{'}}{\tan \gamma\tan \alpha_x{'}} = - \fra... ...^2} = - \frac{k_{y{'}}k_{x{'}_h}k_{x{'}}} {k_z^2 + k_{y{'}}^2}.$$ (18)

The combination of equation (17) and equation (18) enables the computation of 3-D ADCIGs after imaging; using these two relationships, we can map the prestack image from the offset domain $\left(x_h,y_h\right)$to the angle domain $\left(\gamma,\phi\right)$.Notice that the reflection azimuth $\phi$is implicitly included in these equations since, all the wavenumbers, with the exception of k_z, are dependent on $\phi$.Therefore, during computations the wavenumbers need to be properly transformed by rotating the horizontal axes by the azimuth angle $\phi$.

In contrast with the transformation described by equations (9) and (11), the transformation described by equations (17-18) is independent of the local velocity $v\left(z,x,y \right)$.Therefore there is no need to estimate the geological dips locally, but only globally. This estimate can be performed accurately and efficiently in the wavenumber domain. However, it is important to notice that the absence of the local velocity $v\left(z,x,y \right)$ from the expressions used to compute ADCIGs after imaging does not make the result independent from the local migration velocity. This dependence is indirect through the vertical wavenumber k_z; or, in other words, the estimates of $\gamma$ and $\phi$depend on the apparent vertical wavelength of the imaged reflectors. Therefore, the advantages derived from the absence of $v\left(z,x,y \right)$ in equations (17-18) are purely computational. The sensitivity of the estimates of $\gamma$ and $\phi$on the accuracy of the local velocity $v\left(z,x,y \right)$is the same, regardless of whether $\gamma$ and $\phi$ are estimated indirectly through p_xh and p_yh by using equations (9) and (11), or directly by using equations (17-18). This concept is well illustrated by the example shown in the last section (Figures 11-12).

There are two alternative computational algorithms to numerically perform the transformation described by equations (17-18); they differ in whether the computations are performed with the offset axes in the space or wavenumber domain. In either case, it is computationally advantageous to perform the computation in the wavenumber domain $\left(k_z,k_{x},k_{y}\right)$for the physical coordinates, because of the dependence of the mapping on the geological dips. If the ADCIGs are computed for many values of $\gamma$ and $\phi$,it is less expensive to perform the computation in the offset-wavenumber domain by a 3-D generalization of the 2-D radial-trace transform used by Ottolini and Claerbout (1984) and Sava and Fomel (2003). However, this approach can generate artifacts, because the subsurface-offset axes are usually short, and the Fourier transforms have circular boundary conditions. The computation of the slant stack by integration in the offset-space domain avoids these artifacts and can be preferable when high-quality gathers are needed.

 

• Examples of 3-D ADCIGs