




Next: Kinematic properties of 3-D
Up: Angle-Domain Common Image Gathers
Previous: Angle-Domain Common Image Gathers
We start with a simple 2-D qualitative analysis of
the effects of velocity errors on both kinds
of ADCIGs that we presented; that is, ADCIGs computed
before imaging and ADCIGs computed after imaging.
This first step illustrates the sensitivity of the
estimation of the angles 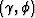 to velocity errors.
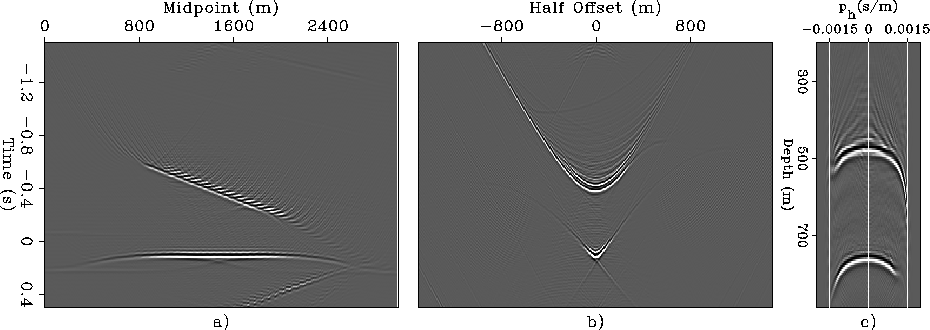
Figure 11
shows the effects of velocity errors on ADCIGs
computed before imaging.
It shows the same panels as
Figure 1
[i.e.
wavefield at zero-offset (a),
wavefield at fixed midpoint (b),
and ADCIG (c)],
but when the migration velocity is 10% higher
than the correct one.
At the correct depth of the flat reflector (z=700 meters),
the energy for both reflectors has started defocusing
and it forms time-reversed hyperbolas.
Most of the energy for the flat reflector has
not reached the zero-time line yet,
causing the flat reflector to be imaged deeper
than the correct depth.
In the ADCIG both events frown downward,
and thus they indicate too high of a migration velocity.
The residual moveout caused by velocity errors
in ADCIGs
is thus qualitatively similar to
the moveout observed in
conventional surface-offset CIGs computed
by Kirchhoff migration.
If the velocity function is too low the reflections
will smile upward;
if the velocity function is too high the reflections
will frown downward.
zoff-cmp-cig-dip-overn-z700-fast
to velocity errors.
Figure 11
shows the effects of velocity errors on ADCIGs
computed before imaging.
It shows the same panels as
Figure 1
[i.e.
wavefield at zero-offset (a),
wavefield at fixed midpoint (b),
and ADCIG (c)],
but when the migration velocity is 10% higher
than the correct one.
At the correct depth of the flat reflector (z=700 meters),
the energy for both reflectors has started defocusing
and it forms time-reversed hyperbolas.
Most of the energy for the flat reflector has
not reached the zero-time line yet,
causing the flat reflector to be imaged deeper
than the correct depth.
In the ADCIG both events frown downward,
and thus they indicate too high of a migration velocity.
The residual moveout caused by velocity errors
in ADCIGs
is thus qualitatively similar to
the moveout observed in
conventional surface-offset CIGs computed
by Kirchhoff migration.
If the velocity function is too low the reflections
will smile upward;
if the velocity function is too high the reflections
will frown downward.
zoff-cmp-cig-dip-overn-z700-fast
Figure 11
Illustration of the sensitivity
to velocity errors of the ADCIGs
computed before imaging.
The panels are the same as in Figure 1;
that is, they display orthogonal slices of the prestack wavefield
after downward continuation to the depth of 700 meters,
but the velocity used for downward continuation
was 10% higher than the correct one.
Panel a) displays the zero-offset section,
panel b) displays the common-midpoint gather at 1,410 meters,
and
panel c) shows the complete (i.e. for all depths)
ADCIG at 1,410 meters.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





off-ang-cig-dip-overn-fast-dz5
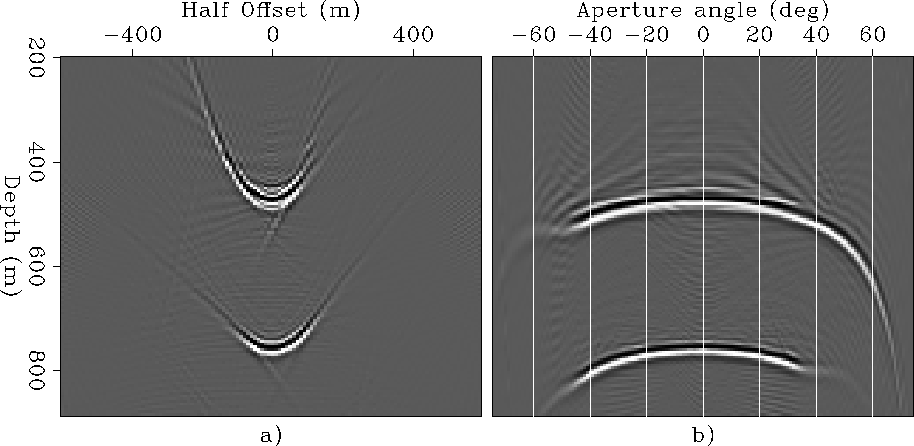
Figure 12
Illustration of the sensitivity of ADCIGs
computed after imaging to velocity errors.
The panels are the same as in Figure 4,
but after migration with a velocity 10% higher than the correct one.
Panel a) displays the ODCIG and panel b) the ADCIG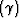 .Notice that the range of
.Notice that the range of 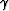 increases from
Figure 4b
to Figure 12b.
increases from
Figure 4b
to Figure 12b.
![[*]](http://sepwww.stanford.edu/latex2html/movie.gif)





Figure 12
shows the effects of velocity errors on ADCIGs
computed after imaging.
It shows the same panels as
Figure 4
[i.e.
ODCIG (a),
and ADCIG (b)],
but when the migration velocity is 10% higher
than the correct one.
The energy is defocused in the ODCIGs
and the events have a hyperbolic moveout
(Figure 12a);
the apexes of the hyperbolas are deeper than the
reflectors' true depths.
Slant stacks transform the hyperbolas into
frowns
(Figure 12b)
that are similar to the
frowns shown in Figure 11c.
However, there is a subtle but important difference
between the two cases.
The pxh range does not change between the ADCIG
shown in
Figure 1c
and the one shown in Figure 11c,
whereas the 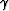 range increases
when the velocity is too high
(Figure 12b).
This increase is due to the increase in the apparent
vertical wavelength in the image,
which correspondingly causes a decrease of kz
in equation (16).
Or, from a different viewpoint,
if we were to use equation (9)
to map pxh into
range increases
when the velocity is too high
(Figure 12b).
This increase is due to the increase in the apparent
vertical wavelength in the image,
which correspondingly causes a decrease of kz
in equation (16).
Or, from a different viewpoint,
if we were to use equation (9)
to map pxh into 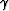 ,the mapping would be affected by both the
increase in
,the mapping would be affected by both the
increase in 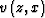 and the increase in
apparent geological dip
and the increase in
apparent geological dip 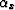 - and the corresponding decrease
in
- and the corresponding decrease
in 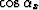 .This simple example illustrates the fact that
the estimates of
.This simple example illustrates the fact that
the estimates of 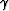 and
and 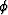 are similarly sensitive
to the accuracy of the local velocity
are similarly sensitive
to the accuracy of the local velocity 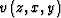 ,regardless of whether ADCIGs are computed
before or after imaging.
,regardless of whether ADCIGs are computed
before or after imaging.





Next: Kinematic properties of 3-D
Up: Angle-Domain Common Image Gathers
Previous: Angle-Domain Common Image Gathers
Stanford Exploration Project
5/23/2004
![]() range increases
when the velocity is too high
(Figure 12b).
This increase is due to the increase in the apparent
vertical wavelength in the image,
which correspondingly causes a decrease of kz
in equation (16).
Or, from a different viewpoint,
if we were to use equation (9)
to map pxh into
range increases
when the velocity is too high
(Figure 12b).
This increase is due to the increase in the apparent
vertical wavelength in the image,
which correspondingly causes a decrease of kz
in equation (16).
Or, from a different viewpoint,
if we were to use equation (9)
to map pxh into ![]() ,the mapping would be affected by both the
increase in
,the mapping would be affected by both the
increase in ![]() and the increase in
apparent geological dip
and the increase in
apparent geological dip ![]() - and the corresponding decrease
in
- and the corresponding decrease
in ![]() .This simple example illustrates the fact that
the estimates of
.This simple example illustrates the fact that
the estimates of ![]() and
and ![]() are similarly sensitive
to the accuracy of the local velocity
are similarly sensitive
to the accuracy of the local velocity ![]() ,regardless of whether ADCIGs are computed
before or after imaging.
,regardless of whether ADCIGs are computed
before or after imaging.