ABSTRACT
When aliased data is slant stacked it sums coherently at
multiple locations in the slowness-frequency (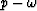 ) domain. Only one of
these locations is the ``true'' location. If the true location can be
distinguished from the aliased locations an unaliased
representation of the data can be computed. The criterion I use
to distinguish between the true dip and the aliased dip is that, for
bandlimited data, the amplitude spectrum at the true dip should be a
locally continuous function of frequency. Once an unaliased
representation of the data has been obtained any slowness domain processing
can be performed before transformation back to the space-time(x-t) domain.
The data can be transformed back to the x-t domain at any
trace spacing to give an dealiased version of the original data. ) domain. Only one of
these locations is the ``true'' location. If the true location can be
distinguished from the aliased locations an unaliased
representation of the data can be computed. The criterion I use
to distinguish between the true dip and the aliased dip is that, for
bandlimited data, the amplitude spectrum at the true dip should be a
locally continuous function of frequency. Once an unaliased
representation of the data has been obtained any slowness domain processing
can be performed before transformation back to the space-time(x-t) domain.
The data can be transformed back to the x-t domain at any
trace spacing to give an dealiased version of the original data.
|
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)
![[*]](http://sepwww.stanford.edu/latex2html/prev_gr.gif)