Constructing an anti-alias mask function

The simple representation of the unaliased energy in the $p-\omega$space suggests a criterion for identifying aliased and unaliased energy. Energy is unaliased if the amplitude spectrum is continuous along a single slowness trace in the $p-\omega$ domain. If the amplitude spectrum changes rapidly along the trace the energy is assumed to be aliased. This is philosophically similar to the approach used by others Zhang et al. (1992) where the zeros of a prediction filter are examined to see if they lie along a line through the origin in the f-k domain.

This criterion will not be reliable if the amplitude spectrum of the wavelet for a particular dip changes rapidly. To overcome this problem I divide the amplitude spectrum for each p-trace by a local normalization factor. This factor is the maximum spectral amplitude over a local window in slowness. After this normalization the amplitude spectrum of the unaliased dip should be a slowly varying function of frequency while the aliased energy will still have a rapidly varying amplitude spectrum. This somewhat ad-hoc method is designed to remove spectral color whilst retaining local amplitude differences. It will fail when events with nearby dips have very different spectra.

I can now generate an ``aliasing'' measure by computing the continuity of the amplitude spectrum as a function of slowness. I calculate an energy normalized smoothness along each slowness trace given by,

The summation is over a running window over frequency. The length of this window should be longer than the bandwidth of the aliased energy on any one trace but shorter than the bandwidth of the unaliased energy. The variable $\delta$ is an energy related damping factor. If it is zero the method is similar to semblance, it will give a measure of smoothness that is independent of the energy along the trace. A high value of $\delta$ will bias the measure towards high amplitude events. I choose a value that is some fraction of the maximum smoothed energy in the whole $p-\omega$ spectrum. The fraction can be varied to allow the user to choose only high energy events or to allow events of all energies.

I generate a mask function by thresholding the smoothness measure. Any point with a value less than the threshold is assumed to be aliased energy and any point with a value greater than the threshold is unaliased energy. I have found that 70% of the maximum value is a reasonable threshold in most circumstances. Figure  shows the four stages in creating the mask function.

 

single-mask
Figure 2 Four stages in creating the mask function. The input spectrum (top-left), the normalized spectrum (top-right), the coherence function (bottom-left), the mask function(bottom-right).

Figure  shows the spectrum of the event in the $p-\omega$ after the mask function has been applied. The aliased energy has been removed and the unaliased energy has been preserved.

 

single-wmask Figure 3 Amplitude spectrum of a single dipping event in the 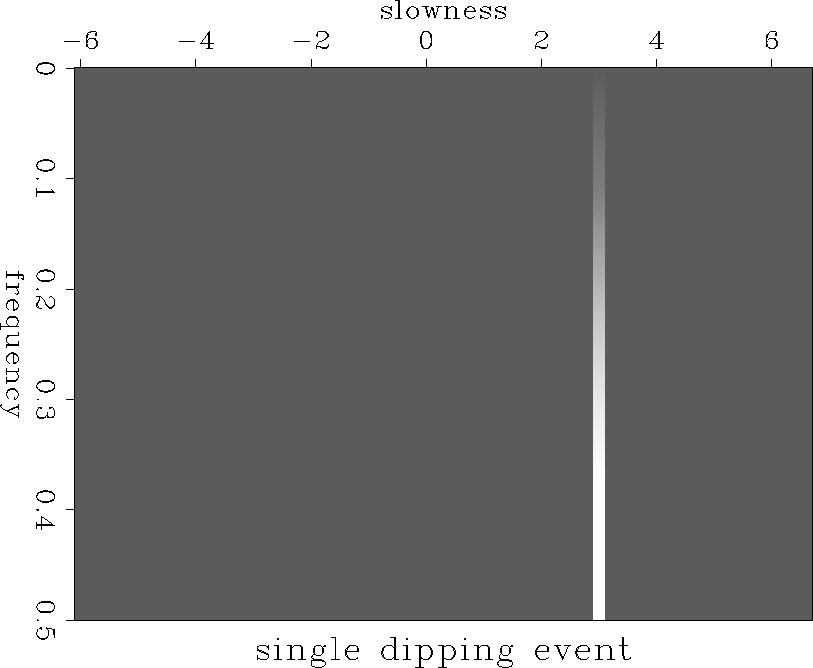$p-\omega$ domain after application of the mask function to remove aliased events.