The effectiveness of this method depends on the amount of overlap
between the unaliased energy at one dip and the aliased energy of
another dip. If all the aliased energy is in the same region as some
unaliased energy it will not be rejected. If the unaliased energy has
a broad dip range e.g. because of event curvature then overlap with
aliased energy is much more likely. One way to reduce the dip-bandwidth of
the ![]() spectrum is to process the data using local windows. The
windows should be designed to include only a few distinguishable dips.
spectrum is to process the data using local windows. The
windows should be designed to include only a few distinguishable dips.
There are two tradeoffs to be considered when designing windows. As
the windows become smaller in time the number of frequencies in the
![]() domain is reduced. When the number of frequencies is
smaller the effectiveness of the continuity detection is reduced. As
the windows become smaller in space the dip resolution of the slant
stack is reduced. The real and aliased events become more spread-out
in slowness and are more likely to interfere.
domain is reduced. When the number of frequencies is
smaller the effectiveness of the continuity detection is reduced. As
the windows become smaller in space the dip resolution of the slant
stack is reduced. The real and aliased events become more spread-out
in slowness and are more likely to interfere.
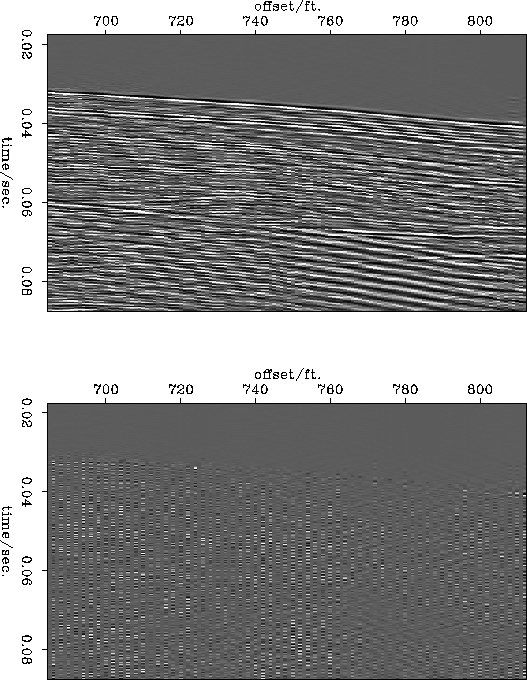
Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) shows the result of reconstructing the
original data using least squares transforms applied in windows on the
data. The windows were 32msec long and 32 ft wide. Each window
overlapped its neighbors on each side by 25%. I used the data
patching algorithm described elsewhere in this report
(). This reconstruction is slightly superior to the one
in figure
shows the result of reconstructing the
original data using least squares transforms applied in windows on the
data. The windows were 32msec long and 32 ft wide. Each window
overlapped its neighbors on each side by 25%. I used the data
patching algorithm described elsewhere in this report
(). This reconstruction is slightly superior to the one
in figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) where the data was all processed together.
where the data was all processed together.
 |
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif)