Berryman: Stratified poroelastic rocks

The mechanics of vertically stratified porous media has some similarities to and some differences from the more typical layered analysis for purely elastic media. Assuming welded solid contact at the solid-solid interfaces implies the usual continuity conditions, which are continuity of the horizontal strain components and the vertical stress components. These conditions are valid for both elastic and poroelastic media. Differences arise through the conditions for the pore pressure and the increment of fluid content in the context of fluid-saturated porous media. 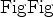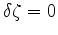The two distinct conditions most typically considered between any pair of contiguous layers are: (1) an undrained fluid condition at the interface, meaning that the increment of fluid content is zero (i.e., $\delta\zeta = 0$ ), or (2) fluid pressure continuity at the interface, implying that the change in fluid pressure is zero across the interface (i.e., $\delta p_f = 0$ ). Depending on the types of measurements being made on the system and the pertinent boundary conditions for these measurements, either (or neither) of these two conditions might be directly pertinent. But these conditions are sufficient nevertheless to be used as thought experiments to determine the expected values of all the poroelastic coefficients. For quasi-static mechanical changes over long time periods, drained conditions hold, so the pressure must then be continuous. For high frequency wave propagation, the fluid typically acts essentially as if it were undrained - or nearly so, with vanishing of the fluid increment at the boundaries being appropriate. The poroelastic analysis of both these end-member cases is treated in detail.

Abstract: