|
|
|
|
Mechanics of stratified anisotropic poroelastic media |
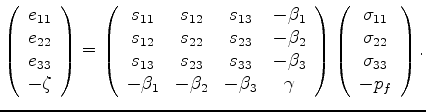 's preceding the stresses and strains,
as is sometimes done to emphasize their smallness, since
this extra notation is truly redundant when they are all being treated
as quantities pertinent to seismic wave propagation
(and therefore resulting in linear effects) as I do here,
for very small deviations from an initial rest state.
's preceding the stresses and strains,
as is sometimes done to emphasize their smallness, since
this extra notation is truly redundant when they are all being treated
as quantities pertinent to seismic wave propagation
(and therefore resulting in linear effects) as I do here,
for very small deviations from an initial rest state.
The ![]() (no summation over repeated indices) are strains in the
(no summation over repeated indices) are strains in the ![]() directions.
The
directions.
The
![]() are the corresponding stresses, assumed to be positive in tension.
The fluid pressure is
are the corresponding stresses, assumed to be positive in tension.
The fluid pressure is ![]() , which is positive in compression. The increment of fluid content
is
, which is positive in compression. The increment of fluid content
is ![]() , and is often defined via:
, and is often defined via:
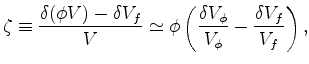 is the pertinent local volume (within a layer in present circumstances)
of the initially fully fluid-saturated porous layer at the first instant of consideration,
is the pertinent local volume (within a layer in present circumstances)
of the initially fully fluid-saturated porous layer at the first instant of consideration,
 's here do indicate small changes in the quantities immediately following them.
For ``drained'' systems, there would ideally be a reservoir of the same fluid just outside
the volume
's here do indicate small changes in the quantities immediately following them.
For ``drained'' systems, there would ideally be a reservoir of the same fluid just outside
the volume 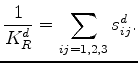 , undrained compliances have replaced
drained compliances in a formula analogous to (4). A similar definition of the effective grain modulus
, undrained compliances have replaced
drained compliances in a formula analogous to (4). A similar definition of the effective grain modulus 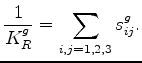 , where
, where
The shear terms due to twisting motions (i.e., strains
![]() ,
, ![]() ,
, ![]() and stresses
and stresses
![]() ,
,
![]() ,
,
![]() ) are excluded from this poroelastic discussion
since they typically do not couple to the modes of interest for anisotropic
systems having orthotropic symmetry, or any more symmetric system such as
those being either transversely isotropic or isotropic.
I have also assumed that the true axes of symmetry are known,
and make use of them in my formulation of the problem.
Note that the
) are excluded from this poroelastic discussion
since they typically do not couple to the modes of interest for anisotropic
systems having orthotropic symmetry, or any more symmetric system such as
those being either transversely isotropic or isotropic.
I have also assumed that the true axes of symmetry are known,
and make use of them in my formulation of the problem.
Note that the ![]() 's are the elements of the compliance
matrix
's are the elements of the compliance
matrix ![]() and are all independent of the fluid, and
therefore would be the same if the medium were treated
as elastic (i.e., by ignoring the fluid pressure, or
assuming that the fluid saturant is air - or vacuum).
In keeping with the earlier discussions, I typically call these compliances
the drained compliances and the corresponding matrix
the drained compliance matrix
and are all independent of the fluid, and
therefore would be the same if the medium were treated
as elastic (i.e., by ignoring the fluid pressure, or
assuming that the fluid saturant is air - or vacuum).
In keeping with the earlier discussions, I typically call these compliances
the drained compliances and the corresponding matrix
the drained compliance matrix ![]() , since the
fluids do not contribute to the stored mechanical energy if they are free to drain
into a surrounding reservoir containing the same type of fluid. In contrast, the
undrained compliance matrix
, since the
fluids do not contribute to the stored mechanical energy if they are free to drain
into a surrounding reservoir containing the same type of fluid. In contrast, the
undrained compliance matrix ![]() presupposes that the fluid is
trapped (unable to drain from the system into an adjacent reservoir) and
therefore contributes in a significant and measurable way to
the compliance and stiffness (
presupposes that the fluid is
trapped (unable to drain from the system into an adjacent reservoir) and
therefore contributes in a significant and measurable way to
the compliance and stiffness (
![]() ), and also
therefore to the stored mechanical energy of the undrained system.
), and also
therefore to the stored mechanical energy of the undrained system.
Although the significance of the formula is somewhat different now, I find again that
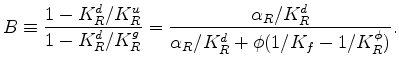 that comes into play when the pores are heterogeneous (Brown and Korringa, 1975),
regardless of whether the system is isotropic or anisotropic.
I emphasize that all these formulas are rigorous statements based on the earlier
anisotropic analyses. The appearance of both the Reuss average quantities
that comes into play when the pores are heterogeneous (Brown and Korringa, 1975),
regardless of whether the system is isotropic or anisotropic.
I emphasize that all these formulas are rigorous statements based on the earlier
anisotropic analyses. The appearance of both the Reuss average quantities
|
|
|
|
Mechanics of stratified anisotropic poroelastic media |