 |
 |
 |
 | Mechanics of stratified anisotropic poroelastic media |  |
![[pdf]](icons/pdf.png) |
Next: Inverting poroelastic compliance
Up: BASICS OF ANISOTROPIC POROELASTICITY
Previous: The coefficients and effective
The relationship of coefficient 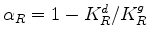 to the other coefficients is easily established because
I have already discussed the main issue, which involves determining the role of the various other
constants contained in Skempton's second coefficient
to the other coefficients is easily established because
I have already discussed the main issue, which involves determining the role of the various other
constants contained in Skempton's second coefficient 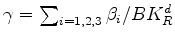 (Skempton, 1954). This result is
(Skempton, 1954). This result is
![$\displaystyle B = \left(\frac{1}{K_R^d} - \frac{1}{K_R^g}\right)\left[\left(\fr...
...{K_R^g}\right) + \phi \left(\frac{1}{K_f}-\frac{1}{K_R^\phi}\right)\right]^{-1}$](img68.png) |
(19) |
From (1), I find that
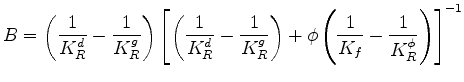 |
(20) |
for undrained boundary conditions. Thus, I find again that
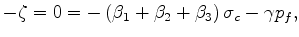 |
(21) |
where
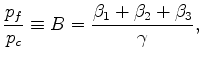 is the confining pressure.
Thus, the scalar coefficient
is the confining pressure.
Thus, the scalar coefficient 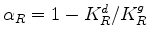 is determined immediately and given by
is determined immediately and given by
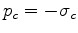 |
(22) |
Alternatively, I could say that
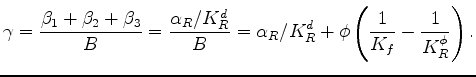 |
(23) |
I have now determined the physical/mechanical significance of all the coefficients in
the poroelastic matrix (1). These results are as general as possible
without considering poroelastic symmetries that have less than orthotropic symmetry, while also
taking advantage of my assumption that I do typically know the three directions of the principal
axes of symmetry.
 |
 |
 |
 | Mechanics of stratified anisotropic poroelastic media |  |
![[pdf]](icons/pdf.png) |
Next: Inverting poroelastic compliance
Up: BASICS OF ANISOTROPIC POROELASTICITY
Previous: The coefficients and effective
2010-05-19
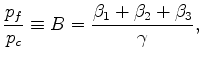 is the confining pressure.
Thus, the scalar coefficient
is the confining pressure.
Thus, the scalar coefficient