|
|
|
|
Mechanics of stratified anisotropic poroelastic media |
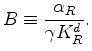 submatrix in the upper left corner of the matrix
in (1) as
submatrix in the upper left corner of the matrix
in (1) as
The resulting ![]() matrix and its inverse are now related by:
matrix and its inverse are now related by:
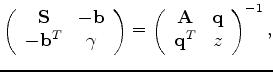 by introducing three components: (a) scalar
by introducing three components: (a) scalar
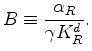 stiffness matrix (i.e., the
pertinent one connecting the principal strains to principal stresses)
is given by
stiffness matrix (i.e., the
pertinent one connecting the principal strains to principal stresses)
is given by
Also, note the important fact that the observed decoupling of the fluid effects occurs only in the compliance form (1) of the equations, and never in the stiffness (inverse) form for the poroelasticity equations.
From these results, it is not hard to show that
There are clearly many measurements required to determine all these various poroelastic coefficients. Furthermore, the strategy for finding the coefficients depends on available data sets, and whether the porous media of interest are constructed from a homogeneous or heterogeneous set of solid materials, and whether the individiual grains are isotropic or anisotropic. It also makes some difference if the pores are approximately rounded (for granular media) or flat (for fractured media). All these issues have been discussed previously at length, and this discussion will not be repeated here.
The remainder of the paper will concentrate on making use of the general poroelastic equations in situations where at least two and possibly many distinct layers of porous materials obeying these equations are under stress (either quasi-static or dynamic as would occur in a wave propagation scenario). As will be shown, the layered poroelastic equations behave somewhat differently from layered elastic equations because there are two distinct additional boundary conditions (drained and undrained) that can occur depending on the details of the excitation itself.
|
|
|
|
Mechanics of stratified anisotropic poroelastic media |