 |
 |
 |
 | Mechanics of stratified anisotropic poroelastic media |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Berryman: Stratified poroelastic rocks
Previous: APPENDIX A: THE SCHOENBERG-MUIR
Using equation (29) as our starting point, I next treat the boundary condition
 for undrained layers (meaning that the fluid is actually physically trapped in the layer, or
the physical process is so fast - such as high frequency wave propagation - that the fluid inertia prevents
rapid movement of fluid particles over non-infinitesimal distances). Depending on the application scenario,
this boundary condition might be applied to all layers, or only to just one or a few layers.
for undrained layers (meaning that the fluid is actually physically trapped in the layer, or
the physical process is so fast - such as high frequency wave propagation - that the fluid inertia prevents
rapid movement of fluid particles over non-infinitesimal distances). Depending on the application scenario,
this boundary condition might be applied to all layers, or only to just one or a few layers.
I consider first a single layer having the undrained boundary condition. For this case, the condition
from Eq. (29) becomes
 |
(59) |
within the layer. Next, the equation can be solved to express the fluid pressure  strain dependence
in each undrained layer (the layer labels are suppressed here for simplicity) as
strain dependence
in each undrained layer (the layer labels are suppressed here for simplicity) as
 |
(60) |
Then, substituting this condition back into the expressions for 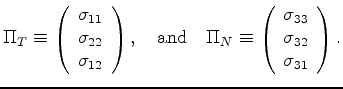 and
and 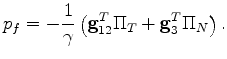 from
(29), I find that
from
(29), I find that
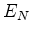 |
(61) |
To understand the significance of (61), I next consider
that it is straightforward to show that each of these composite matrix elements
corresponds exactly to the undrained version of the Schoenberg-Muir matrices. So that,
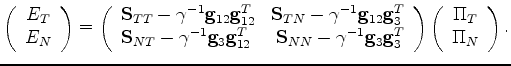 |
(62) |
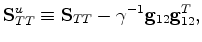 |
(63) |
and
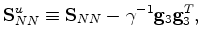 |
(64) |
All these expressions follow directly from the form of (61).
Thus, I arrive at a result that might have been anticipated, which is that the undrained layers
respond according to the usual undrained conditions in each individual layer. The part of the result
that is new concerns the forms of the undrained matrices
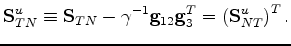 ,
,
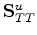 , and
, and
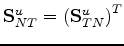 , in the now modified Schoenberg-Muir formalism.
, in the now modified Schoenberg-Muir formalism.
This analogy can be pushed somewhat further to include the effective values for the undrained moduli
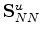 ,
,
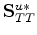 , and
, and
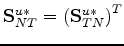 , with
formulas entirely analogous to (49), (50), and
(53), and undrained constants replacing drained constants everywhere.
Since there is nothing subtle about this step, I will therefore leave these details
to be filled in by the interested reader.
, with
formulas entirely analogous to (49), (50), and
(53), and undrained constants replacing drained constants everywhere.
Since there is nothing subtle about this step, I will therefore leave these details
to be filled in by the interested reader.
 |
 |
 |
 | Mechanics of stratified anisotropic poroelastic media |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Berryman: Stratified poroelastic rocks
Previous: APPENDIX A: THE SCHOENBERG-MUIR
2010-05-19
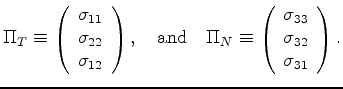 and
and 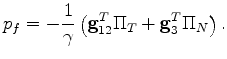 from
(29), I find that
from
(29), I find that
![]() ,
,
![]() , and
, and
![]() , in the now modified Schoenberg-Muir formalism.
, in the now modified Schoenberg-Muir formalism.
![]() ,
,
![]() , and
, and
![]() , with
formulas entirely analogous to (49), (50), and
(53), and undrained constants replacing drained constants everywhere.
Since there is nothing subtle about this step, I will therefore leave these details
to be filled in by the interested reader.
, with
formulas entirely analogous to (49), (50), and
(53), and undrained constants replacing drained constants everywhere.
Since there is nothing subtle about this step, I will therefore leave these details
to be filled in by the interested reader.