|
|
|
|
Wave-equation tomography by beam focusing |
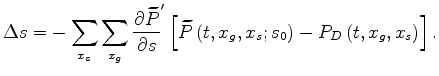 and
and Figure 2 illustrates the limitations of full-waveform inversion when applied to estimating the background velocity. I therefore applied the proposed method to the case with a large velocity error, to demonstrate that it overcomes these limitations of full-waveform inversion.
Figure 3
shows the derivatives of the objective function
with respect to the moveout parameters computed using
equations 16-17
and 18-19.
The plot in panel a) displays the derivatives with respect
to the local curvature, ![]() ;
the plot in panel b) displays
the derivatives with respect to the time shifts of the beam centers,
;
the plot in panel b) displays
the derivatives with respect to the time shifts of the beam centers,
![]() .
In both cases the derivatives are plotted as a function of the
beam center coordinate,
.
In both cases the derivatives are plotted as a function of the
beam center coordinate,
![]() , for the source location at
, for the source location at
![]() km; that is, in the middle of the model.
As visible from the figure, I clipped to zero the derivatives
for both parameters outside
of the
km; that is, in the middle of the model.
As visible from the figure, I clipped to zero the derivatives
for both parameters outside
of the
![]() km range
to avoid edge effects.
km range
to avoid edge effects.
Figure 3a clearly shows that the local curvature is an appropriate parameters to measure the effects of large-scale velocity errors. In contrast, the alternating signs of the time shift derivatives shown in Figure 3b demonstrates that such perturbations are not well captured by the global moveout parameters.
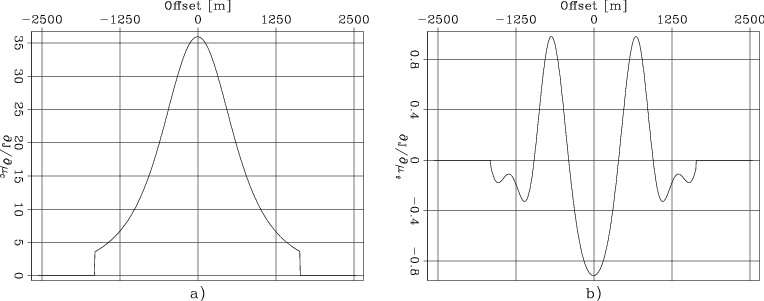
These observations are confirmed by Figures 4 and 5. Figure 4 shows the search direction computed using equation 24. In contrast with the search direction computed with conventional waveform inversion (Figure 2), the search direction shown in Figure 4 has the correct polarity. It provides a good search direction, similar to the one provided by full-waveform inversion with the small velocity error that is shown in Figure 1.
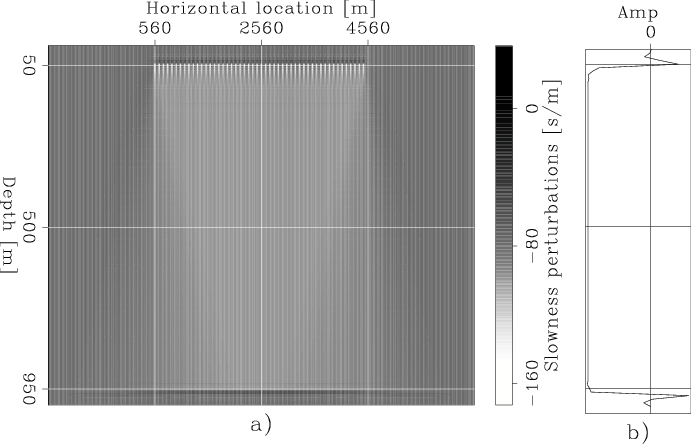
The search direction obtained by computing the gradient of the global objective function using equation 25 is shown in Figure 5. It shows strong edge effects and its horizontal average (Figure 5b)) has the wrong polarity.
|
Beam-DC-DT-large-neg
Figure 3. Derivatives of the objective functions with respect to the moveout parameters plotted as a function of beam center coordinate, |
|
|---|---|
|
|
|
Avg-Dir-Beam-large-neg
Figure 4. Search direction computed using the gradient of the local objective function |
|
|---|---|
|
|
|
Avg-Dir-Glob-Beam-large-neg
Figure 5. Search direction computed using the gradient of the global objective function |
|
|---|---|
|
|
|
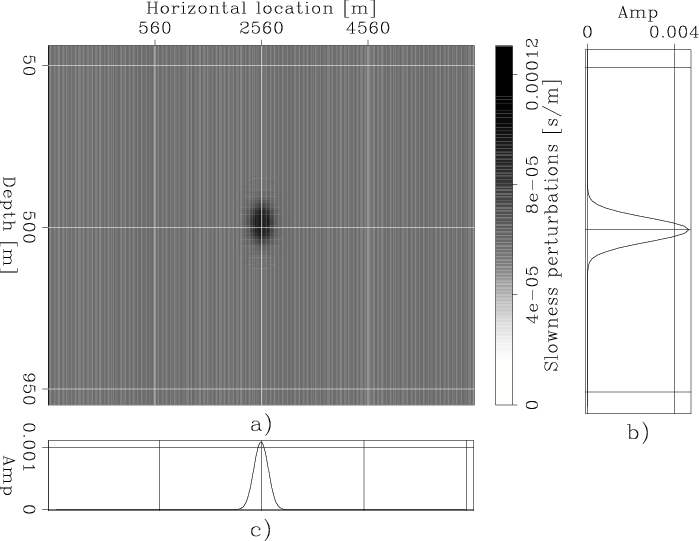
VH-Avg-DSlow-panom
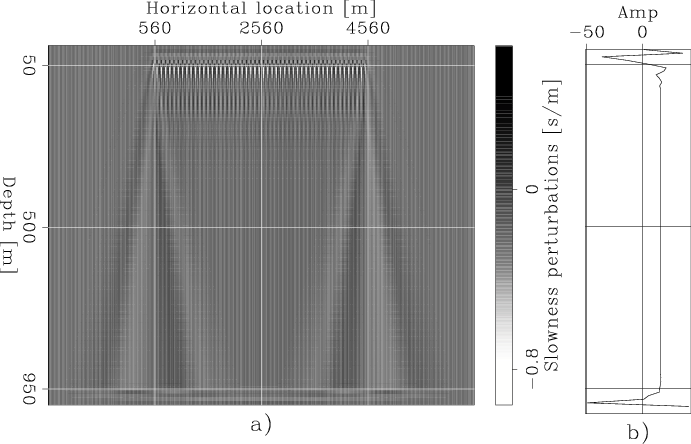
Figure 6. The slowness error that was assumed for the background slowness model |
|
|---|---|
|
|
|
|
|
|
Wave-equation tomography by beam focusing |