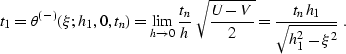Next: Offset continuation and DMO
Up: Offset continuation for reflection
Previous: Kirchhoff model and the
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes a continuous process of
reflected wavefield continuation in the time-offset-midpoint domain.
In order to find an integral-type operator that performs the one-step
offset continuation, I consider the following initial-value (Cauchy)
problem for equation (
) describes a continuous process of
reflected wavefield continuation in the time-offset-midpoint domain.
In order to find an integral-type operator that performs the one-step
offset continuation, I consider the following initial-value (Cauchy)
problem for equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
Given a post-NMO constant-offset section at half-offset h1
| 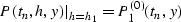 |
(219) |
and its first-order derivative with respect to offset
| 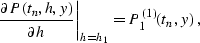 |
(220) |
find the corresponding section P(0)(tn,y) at offset h.
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) belongs to the hyperbolic type, with
the offset coordinate h being a ``time-like'' variable and the
midpoint coordinate y and the time tn being ``space-like''
variables. The last condition (
) belongs to the hyperbolic type, with
the offset coordinate h being a ``time-like'' variable and the
midpoint coordinate y and the time tn being ``space-like''
variables. The last condition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is required for the
initial value problem to be well-posed Courant (1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (
) is required for the
initial value problem to be well-posed Courant (1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (
), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
The integral solution of problem (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
for equation (
)
for equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is obtained in
Appendix
) is obtained in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with the help of the classic methods of
mathematical physics. It takes the explicit form
with the help of the classic methods of
mathematical physics. It takes the explicit form
| 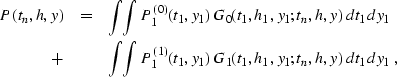 |
|
| (221) |
where the Green's functions G0 and G1 are expressed as
| 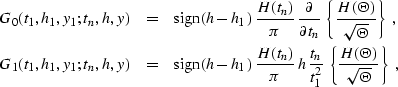 |
(222) |
| (223) |
and the parameter 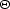 is
is
| 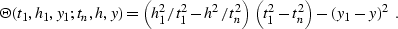 |
(224) |
H stands for the Heavyside step-function.
From equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) one can see
that the impulse response of the offset continuation operator is
discontinuous in the time-offset-midpoint space on a surface defined
by the equality
) one can see
that the impulse response of the offset continuation operator is
discontinuous in the time-offset-midpoint space on a surface defined
by the equality
| 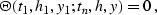 |
(225) |
which describes the ``wavefronts'' of the offset continuation process.
In terms of the theory of characteristics Courant (1962), the surface
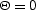 corresponds to the characteristic conoid formed by the
bi-characteristics of equation (
corresponds to the characteristic conoid formed by the
bi-characteristics of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - time rays
emerging from the point
) - time rays
emerging from the point 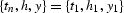 . The
common-offset slices of the characteristic conoid are shown in the
left plot of Figure
. The
common-offset slices of the characteristic conoid are shown in the
left plot of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
con
.
con
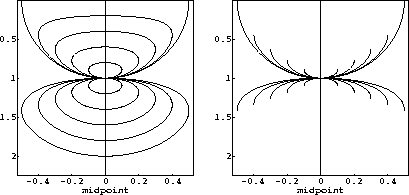
Figure 7
Constant-offset sections of the characteristic conoid - ``offset
continuation fronts'' (left), and branches of the conoid used in the
integral OC operator (right). The upper part of the plots
(small times) corresponds to continuation to smaller offsets; the
lower part (large times) corresponds to larger offsets.





As a second-order differential equation of the hyperbolic type,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes two different processes. The
first process is ``forward'' continuation from smaller to larger
offsets, the second one is ``reverse'' continuation in the opposite
direction. These two processes are clearly separated in the
high-frequency asymptotics of operator (
) describes two different processes. The
first process is ``forward'' continuation from smaller to larger
offsets, the second one is ``reverse'' continuation in the opposite
direction. These two processes are clearly separated in the
high-frequency asymptotics of operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). To obtain
the asymptotical representation, it is sufficient to note that
). To obtain
the asymptotical representation, it is sufficient to note that 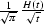 is the impulse response
of the causal half-order integration operator and that
is the impulse response
of the causal half-order integration operator and that 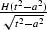 is asymptotically equivalent to
is asymptotically equivalent to 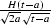 (t, a >0). Thus, the asymptotical form of
the integral offset-continuation operator becomes
(t, a >0). Thus, the asymptotical form of
the integral offset-continuation operator becomes
| 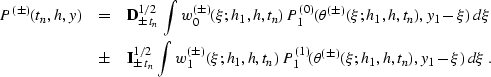 |
|
| (226) |
Here the signs ``+'' and ``-'' correspond to the type of
continuation (the sign of h-h1), 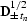 and
and
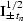 stand for the operators of causal and
anticausal half-order differentiation and integration applied with
respect to the time variable tn, the summation paths
stand for the operators of causal and
anticausal half-order differentiation and integration applied with
respect to the time variable tn, the summation paths
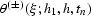 correspond to the two non-negative
sections of the characteristic conoid (
correspond to the two non-negative
sections of the characteristic conoid (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) (Figure
) (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
| 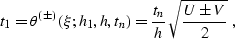 |
(227) |
where 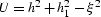 , and
, and 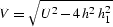 ;
; 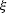 is
the midpoint separation (the integration parameter), and
is
the midpoint separation (the integration parameter), and 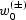 and
and 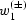 are the following weighting functions:
are the following weighting functions:
| 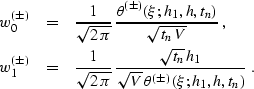 |
(228) |
| (229) |
Expression (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the summation path of the OC
operator was obtained previously by Stovas and Fomel (1993, 1996) and
Biondi and Chemingui (1994a,b). A somewhat different form of it
is proposed by Bagaini and Spagnolini (1996). I describe the kinematic
interpretation of formula (
) for the summation path of the OC
operator was obtained previously by Stovas and Fomel (1993, 1996) and
Biondi and Chemingui (1994a,b). A somewhat different form of it
is proposed by Bagaini and Spagnolini (1996). I describe the kinematic
interpretation of formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in
Appendix
) in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
In the high-frequency asymptotics, it is possible to replace the two
terms in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with a single term
Fomel (1996b). The single-term expression is
) with a single term
Fomel (1996b). The single-term expression is
| 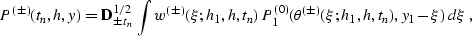 |
(230) |
where
| 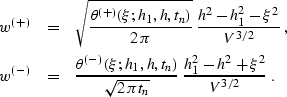 |
(231) |
| (232) |
A more general approach to true-amplitude asymptotic offset
continuation is developed by Santos et al. (1997).
The limit of expression (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the output offset h
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
Deregowski and Rocca (1981)
) for the output offset h
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
Deregowski and Rocca (1981)
| 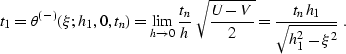 |
(233) |
I discuss the connection between offset continuation and DMO in the
next section.





Next: Offset continuation and DMO
Up: Offset continuation for reflection
Previous: Kirchhoff model and the
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes a continuous process of
reflected wavefield continuation in the time-offset-midpoint domain.
In order to find an integral-type operator that performs the one-step
offset continuation, I consider the following initial-value (Cauchy)
problem for equation (
) describes a continuous process of
reflected wavefield continuation in the time-offset-midpoint domain.
In order to find an integral-type operator that performs the one-step
offset continuation, I consider the following initial-value (Cauchy)
problem for equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) belongs to the hyperbolic type, with
the offset coordinate h being a ``time-like'' variable and the
midpoint coordinate y and the time tn being ``space-like''
variables. The last condition (
) belongs to the hyperbolic type, with
the offset coordinate h being a ``time-like'' variable and the
midpoint coordinate y and the time tn being ``space-like''
variables. The last condition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is required for the
initial value problem to be well-posed Courant (1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (
) is required for the
initial value problem to be well-posed Courant (1962). From a physical
point of view, its role is to separate the two different wave-like
processes embedded in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (
), which are
analogous to inward and outward wave propagation. We will associate
the first process with continuation to a larger offset and the second
one with continuation to a smaller offset. Though the offset
derivatives of data are not measured in practice, they can be
estimated from the data at neighboring offsets by a finite-difference
approximation. Selecting a propagation branch explicitly, for example
by considering the high-frequency asymptotics of the continuation
operators, can allow us to eliminate the need for
condition (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
). In this section, I discuss the exact
integral solution of the OC equation and analyze its asymptotics.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
for equation (
)
for equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is obtained in
Appendix
) is obtained in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) with the help of the classic methods of
mathematical physics. It takes the explicit form
with the help of the classic methods of
mathematical physics. It takes the explicit form
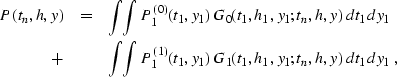
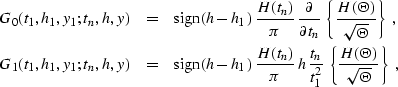
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) one can see
that the impulse response of the offset continuation operator is
discontinuous in the time-offset-midpoint space on a surface defined
by the equality
) one can see
that the impulse response of the offset continuation operator is
discontinuous in the time-offset-midpoint space on a surface defined
by the equality
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) - time rays
emerging from the point
) - time rays
emerging from the point ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes two different processes. The
first process is ``forward'' continuation from smaller to larger
offsets, the second one is ``reverse'' continuation in the opposite
direction. These two processes are clearly separated in the
high-frequency asymptotics of operator (
) describes two different processes. The
first process is ``forward'' continuation from smaller to larger
offsets, the second one is ``reverse'' continuation in the opposite
direction. These two processes are clearly separated in the
high-frequency asymptotics of operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). To obtain
the asymptotical representation, it is sufficient to note that
). To obtain
the asymptotical representation, it is sufficient to note that ![]() is the impulse response
of the causal half-order integration operator and that
is the impulse response
of the causal half-order integration operator and that ![]() is asymptotically equivalent to
is asymptotically equivalent to ![]() (t, a >0). Thus, the asymptotical form of
the integral offset-continuation operator becomes
(t, a >0). Thus, the asymptotical form of
the integral offset-continuation operator becomes
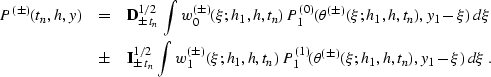
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) (Figure
) (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ):
):
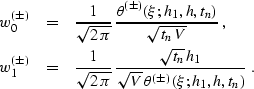
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the summation path of the OC
operator was obtained previously by Stovas and Fomel (1993, 1996) and
Biondi and Chemingui (1994a,b). A somewhat different form of it
is proposed by Bagaini and Spagnolini (1996). I describe the kinematic
interpretation of formula (
) for the summation path of the OC
operator was obtained previously by Stovas and Fomel (1993, 1996) and
Biondi and Chemingui (1994a,b). A somewhat different form of it
is proposed by Bagaini and Spagnolini (1996). I describe the kinematic
interpretation of formula (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in
Appendix
) in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with a single term
Fomel (1996b). The single-term expression is
) with a single term
Fomel (1996b). The single-term expression is
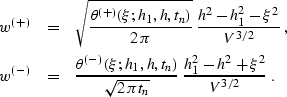
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for the output offset h
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
Deregowski and Rocca (1981)
) for the output offset h
approaching zero can be evaluated by L'Hospitale's rule. As one would
expect, it coincides with the well-known expression for the summation
path of the integral DMO operator
Deregowski and Rocca (1981)