




Next: The kinematics of offset
Up: Three-dimensional seismic data regularization
Previous: Second-order reflection traveltime derivatives
Solving the Cauchy problem
To obtain an explicit solution of the Cauchy
problem (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for
equation (
) for
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), it is convenient to apply the
following simple transform of the wavefield P:
), it is convenient to apply the
following simple transform of the wavefield P:
| 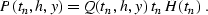 |
(287) |
Here the Heavyside function H is included to take into account the
causality of the reflection seismic gathers (note that the time
tn=0 corresponds to the direct wave arrival). We can extrapolate
Q as an even function to negative times, writing the reverse of
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as follows:
) as follows:
| 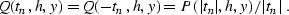 |
(288) |
With the change of function (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), equation (
), equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
transforms to
)
transforms to
| 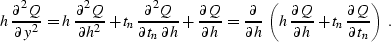 |
(289) |
Applying the change of variables
| 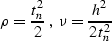 |
(290) |
and Fourier transform in the midpoint coordinate y
| 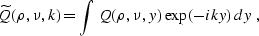 |
(291) |
I further transform equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the canonical form of a
hyperbolic-type partial differential equation with two variables:
) to the canonical form of a
hyperbolic-type partial differential equation with two variables:
| 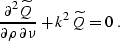 |
(292) |
rim
Figure 1
Domain of dependence of a point in the transformed coordinate system.
|
| 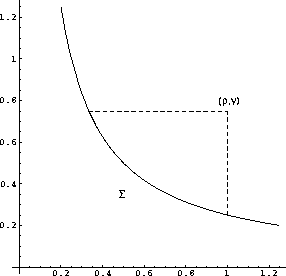 |

The initial value conditions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
) in the
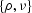 space are defined on a hyperbola of the form
space are defined on a hyperbola of the form
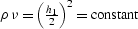 . Now the solution
of the Cauchy problem follows directly from Riemann's method Courant (1962).
According to this method, the domain of dependence of each point
. Now the solution
of the Cauchy problem follows directly from Riemann's method Courant (1962).
According to this method, the domain of dependence of each point
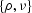 is a part of the hyperbola between the points
is a part of the hyperbola between the points
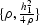 and
and 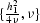 (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If we let
). If we let  denote this curve, the solution takes an explicit integral form:
denote this curve, the solution takes an explicit integral form:
| 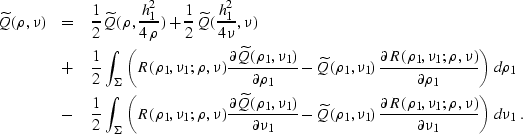 |
|
| |
| (293) |
Here R is the Riemann's function of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which has
the known explicit analytical expression
), which has
the known explicit analytical expression
| 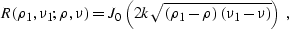 |
(294) |
where J0 is the Bessel function of zeroth order. Integrating by
parts and taking into account the connection of the variables on the
curve  , we can simplify equation (
, we can simplify equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the form
) to the form
| 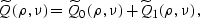 |
(295) |
where
| 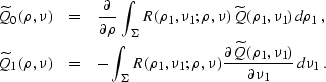 |
(296) |
| (297) |
Applying the explicit expression for the Riemann function R
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and performing the inverse transform of both the
function and the variables allows us to rewrite equations
(
) and performing the inverse transform of both the
function and the variables allows us to rewrite equations
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the original
coordinate system. This yields the integral offset continuation
operators in the
) in the original
coordinate system. This yields the integral offset continuation
operators in the 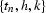 domain
domain
| 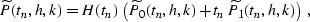 |
(298) |
where
| 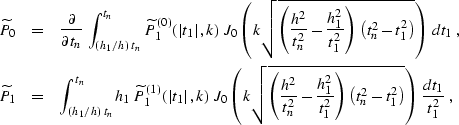 |
(299) |
| (300) |
| 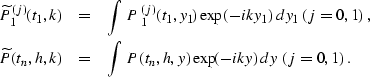 |
(301) |
| (302) |
The inverse Fourier transforms of equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are reduced to analytically evaluated integrals
Gradshtein and Ryzhik (1994) to produce explicit integral operators in the
time-and-space domain
) are reduced to analytically evaluated integrals
Gradshtein and Ryzhik (1994) to produce explicit integral operators in the
time-and-space domain
| 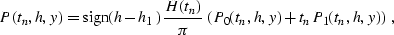 |
(303) |
where
| 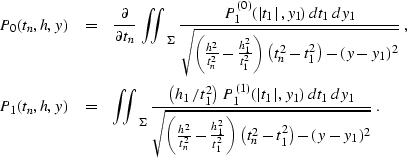 |
(304) |
| (305) |
The range of integration 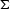 in (
in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
defined by the inequality
) is
defined by the inequality
| 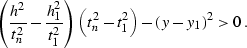 |
(306) |
Equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
coincide with (
)
coincide with (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and
(
), and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the main text.
) in the main text.





Next: The kinematics of offset
Up: Three-dimensional seismic data regularization
Previous: Second-order reflection traveltime derivatives
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) -
-![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for
equation (
) for
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), it is convenient to apply the
following simple transform of the wavefield P:
), it is convenient to apply the
following simple transform of the wavefield P:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as follows:
) as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), equation (
), equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
transforms to
)
transforms to
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the canonical form of a
hyperbolic-type partial differential equation with two variables:
) to the canonical form of a
hyperbolic-type partial differential equation with two variables:

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
) in the
![]() space are defined on a hyperbola of the form
space are defined on a hyperbola of the form
![]() . Now the solution
of the Cauchy problem follows directly from Riemann's method Courant (1962).
According to this method, the domain of dependence of each point
. Now the solution
of the Cauchy problem follows directly from Riemann's method Courant (1962).
According to this method, the domain of dependence of each point
![]() is a part of the hyperbola between the points
is a part of the hyperbola between the points
![]() and
and ![]() (Figure
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If we let
). If we let ![]() denote this curve, the solution takes an explicit integral form:
denote this curve, the solution takes an explicit integral form:
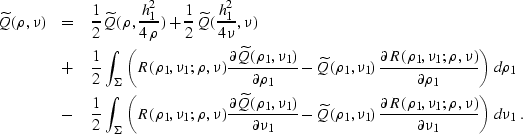
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which has
the known explicit analytical expression
), which has
the known explicit analytical expression
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the form
) to the form
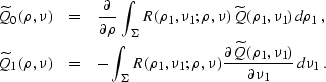
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and performing the inverse transform of both the
function and the variables allows us to rewrite equations
(
) and performing the inverse transform of both the
function and the variables allows us to rewrite equations
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the original
coordinate system. This yields the integral offset continuation
operators in the
) in the original
coordinate system. This yields the integral offset continuation
operators in the ![]() domain
domain
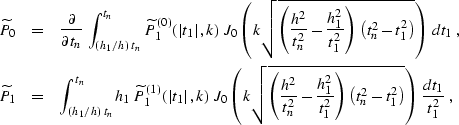
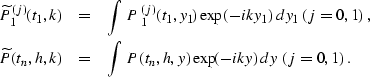
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are reduced to analytically evaluated integrals
Gradshtein and Ryzhik (1994) to produce explicit integral operators in the
time-and-space domain
) are reduced to analytically evaluated integrals
Gradshtein and Ryzhik (1994) to produce explicit integral operators in the
time-and-space domain
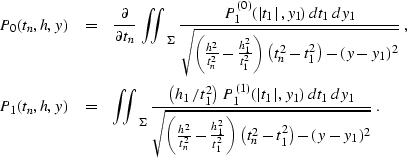
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
defined by the inequality
) is
defined by the inequality
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
coincide with (
)
coincide with (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), (
), (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and
(
), and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the main text.
) in the main text.