




Next: REFERENCES
Up: Three-dimensional seismic data regularization
Previous: Solving the Cauchy problem
The kinematics of offset continuation
In this Appendix, I apply an alternative method to derive equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which describes the summation path of the
integral offset continuation operator. The method is based on the
following considerations.
), which describes the summation path of the
integral offset continuation operator. The method is based on the
following considerations.
The summation path of an integral (stacking) operator coincides with
the phase function of the impulse response of the inverse operator.
Impulse response is by definition the operator reaction to an impulse
in the input data. For the case of offset continuation, the input is a
reflection common-offset gather. From the physical point of view, an
impulse in this type of data corresponds to the special focusing
reflector (elliptical isochrone) at the depth. Therefore, reflection
from this reflector at a different constant offset corresponds to the
impulse response of the OC operator. In other words, we can view
offset continuation as the result of cascading prestack common-offset
migration, which produces the elliptic surface, and common-offset
modeling (inverse migration) for different offsets. This approach
resemble that of Deregowski and Rocca 1981.
It was also applied to a more general case of azimuth moveout (AMO) by
Fomel and Biondi 1995b. The geometric approach implies that
in order to find the summation pass of the OC operator, one should
solve the kinematic problem of reflection from an elliptic reflector
whose focuses are in the shot and receiver locations of the output
seismic gather.
In order to solve this problem , let us consider an elliptic surface of
the general form
| 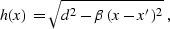 |
(307) |
where 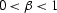 . In a constant velocity medium, the reflection
ray path for a given source-receiver pair on the surface is controlled
by the position of the reflection point x. Fermat's principle
provides a required constraint for finding this position. According to
Fermat's principle, the reflection ray path corresponds to a
stationary value of the travel-time. Therefore, in the neighborhood of
this path,
. In a constant velocity medium, the reflection
ray path for a given source-receiver pair on the surface is controlled
by the position of the reflection point x. Fermat's principle
provides a required constraint for finding this position. According to
Fermat's principle, the reflection ray path corresponds to a
stationary value of the travel-time. Therefore, in the neighborhood of
this path,
| 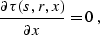 |
(308) |
where s and r stand for the source and receiver locations on the
surface, and  is the reflection traveltime
is the reflection traveltime
| 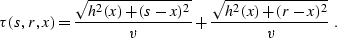 |
(309) |
Substituting (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) leads to a
quadratic algebraic equation on the reflection point parameter x.
This equation has the explicit solution
) leads to a
quadratic algebraic equation on the reflection point parameter x.
This equation has the explicit solution
| 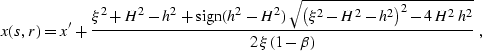 |
(310) |
where h=(r-s)/2, 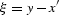 , y=(s+r)/2, and
, y=(s+r)/2, and 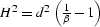 . Replacing x in equation
(
. Replacing x in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with its expression (
) with its expression (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) solves
the kinematic part of the problem, producing the explicit traveltime
expression
) solves
the kinematic part of the problem, producing the explicit traveltime
expression
| 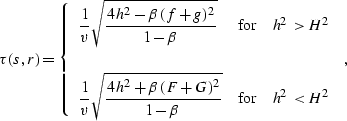 |
(311) |
where
The two branches of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) correspond to the
difference in the geometry of the reflected rays in two different
situations. When a source-and-receiver pair is inside the focuses of
the elliptic reflector, the midpoint y and the reflection point x
are on the same side of the ellipse with respect to its small
semi-axis. They are on different sides in the opposite case (Figure
) correspond to the
difference in the geometry of the reflected rays in two different
situations. When a source-and-receiver pair is inside the focuses of
the elliptic reflector, the midpoint y and the reflection point x
are on the same side of the ellipse with respect to its small
semi-axis. They are on different sides in the opposite case (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).
ell
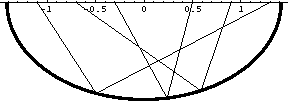
Figure 2
Reflections from an ellipse. The three pairs of reflected rays
correspond to a common midpoint (at 0.1) and different offsets. The
focuses of the ellipse are at 1 and -1.
|
|  |





If we apply the NMO correction, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed to
) is transformed to
| 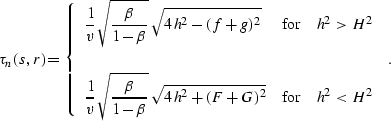 |
(312) |
Then, recalling the relationships between the parameters of the
focusing ellipse r, x' and 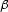 and the parameters of the
output seismic gather Deregowski and Rocca (1981)
and the parameters of the
output seismic gather Deregowski and Rocca (1981)
| 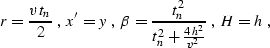 |
(313) |
and substituting expressions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into equation
(
) into equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields the expression
) yields the expression
| 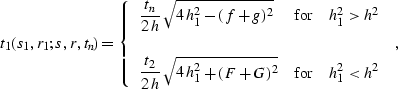 |
(314) |
where
It is easy to verify algebraically the mathematical equivalence of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and equation (
) and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
main text. The kinematic approach described in this appendix applies
equally well to different acquisition configurations of the input and
output data. The source-receiver parameterization used in
(
) in the
main text. The kinematic approach described in this appendix applies
equally well to different acquisition configurations of the input and
output data. The source-receiver parameterization used in
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the actual definition for the summation path of
the integral shot continuation operator
Bagaini and Spagnolini (1993, 1996); Schwab (1993). A family of
these summation curves is shown in Figure
) is the actual definition for the summation path of
the integral shot continuation operator
Bagaini and Spagnolini (1993, 1996); Schwab (1993). A family of
these summation curves is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
shc
Figure 3
Summation paths of the integral shot continuation. The output source
is at -0.5 km. The output receiver is at 0.5 km. The indexes of the
curves correspond to the input source location.










Next: REFERENCES
Up: Three-dimensional seismic data regularization
Previous: Solving the Cauchy problem
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which describes the summation path of the
integral offset continuation operator. The method is based on the
following considerations.
), which describes the summation path of the
integral offset continuation operator. The method is based on the
following considerations.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) leads to a
quadratic algebraic equation on the reflection point parameter x.
This equation has the explicit solution
) leads to a
quadratic algebraic equation on the reflection point parameter x.
This equation has the explicit solution
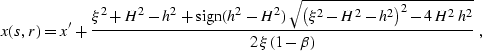
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with its expression (
) with its expression (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) solves
the kinematic part of the problem, producing the explicit traveltime
expression
) solves
the kinematic part of the problem, producing the explicit traveltime
expression
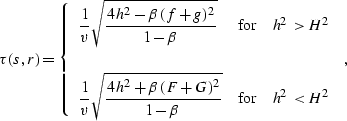
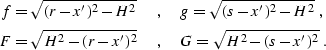
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) correspond to the
difference in the geometry of the reflected rays in two different
situations. When a source-and-receiver pair is inside the focuses of
the elliptic reflector, the midpoint y and the reflection point x
are on the same side of the ellipse with respect to its small
semi-axis. They are on different sides in the opposite case (Figure
) correspond to the
difference in the geometry of the reflected rays in two different
situations. When a source-and-receiver pair is inside the focuses of
the elliptic reflector, the midpoint y and the reflection point x
are on the same side of the ellipse with respect to its small
semi-axis. They are on different sides in the opposite case (Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).

![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is transformed to
) is transformed to
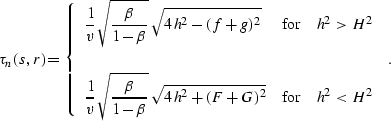
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into equation
(
) into equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) yields the expression
) yields the expression
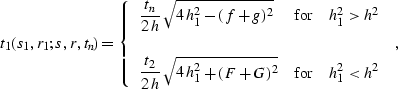
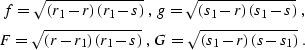
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and equation (
) and equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the
main text. The kinematic approach described in this appendix applies
equally well to different acquisition configurations of the input and
output data. The source-receiver parameterization used in
(
) in the
main text. The kinematic approach described in this appendix applies
equally well to different acquisition configurations of the input and
output data. The source-receiver parameterization used in
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the actual definition for the summation path of
the integral shot continuation operator
Bagaini and Spagnolini (1993, 1996); Schwab (1993). A family of
these summation curves is shown in Figure
) is the actual definition for the summation path of
the integral shot continuation operator
Bagaini and Spagnolini (1993, 1996); Schwab (1993). A family of
these summation curves is shown in Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
.
