




Next: Offset continuation in the
Up: Offset continuation for reflection
Previous: The Cauchy problem and
Dip moveout represents a particular case of offset continuation for
the output offset equal to zero. In this section, I consider the DMO
case separately in order to compare the solutions of equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
Starting from equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in
Appendix
) in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and setting the output offset to zero,
we obtain the following DMO-like integral operators in the t-k
domain:
and setting the output offset to zero,
we obtain the following DMO-like integral operators in the t-k
domain:
| 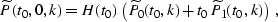 |
(234) |
where
| 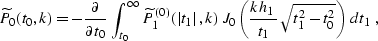 |
(235) |
| 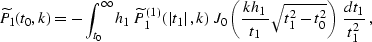 |
(236) |
the wavenumber k corresponds to the midpoint axis y, and J0 is
the zeroth-order Bessel function. The Fourier transform
of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to the time variable
t0 reduces to known integrals Gradshtein and Ryzhik (1994) and creates explicit
DMO-type operators in the frequency-wavenumber domain, as follows:
) with respect to the time variable
t0 reduces to known integrals Gradshtein and Ryzhik (1994) and creates explicit
DMO-type operators in the frequency-wavenumber domain, as follows:
| 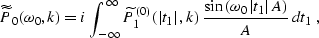 |
(237) |
| 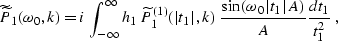 |
(238) |
where
| 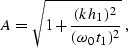 |
(239) |
| 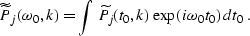 |
(240) |
It is interesting to note that the first term of the continuation to
zero offset (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) coincides exactly with the imaginary part
of Hale's DMO operator Hale (1984). However, unlike Hale's,
operator (
) coincides exactly with the imaginary part
of Hale's DMO operator Hale (1984). However, unlike Hale's,
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is causal, which means that its impulse
response does not continue to negative times. The non-causality of
Hale's DMO and related issues are discussed in more detail by
Stovas and Fomel (1996) and Fomel (1995b).
) is causal, which means that its impulse
response does not continue to negative times. The non-causality of
Hale's DMO and related issues are discussed in more detail by
Stovas and Fomel (1996) and Fomel (1995b).
Though Hale's DMO is known to provide correct reconstruction of the
geometry of zero-offset reflections, it does not account properly for
the amplitude changes Black et al. (1993). The preceding section of this
chapter shows that the additional contribution to the amplitude
is contained in the second term of the OC operator
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which transforms to the second term in the DMO
operator (
), which transforms to the second term in the DMO
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Note that this term vanishes at the input offset
equal to zero, which represents the case of the inverse DMO operator.
). Note that this term vanishes at the input offset
equal to zero, which represents the case of the inverse DMO operator.
Considering the inverse DMO operator as the continuation from zero
offset to a non-zero offset, we can obtain its representation in the
t-k domain from equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
| 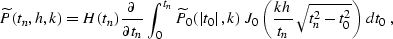 |
(241) |
Fourier transforming equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to the time
variable t0 according to equation (
) with respect to the time
variable t0 according to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we get the
Fourier-domain version of the ``amplitude-preserving'' inverse DMO:
), we get the
Fourier-domain version of the ``amplitude-preserving'' inverse DMO:
| 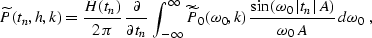 |
(242) |
| 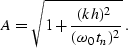 |
(243) |
Comparing operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with Ronen's version of inverse DMO
Ronen (1987), one can see that if Hale's DMO is denoted
by
) with Ronen's version of inverse DMO
Ronen (1987), one can see that if Hale's DMO is denoted
by 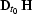 , then Ronen's inverse DMO is
, then Ronen's inverse DMO is 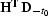 , while the amplitude-preserving inverse (
, while the amplitude-preserving inverse (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is
)
is 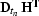 . Here
. Here 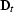 is the derivative
operator
is the derivative
operator 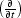 , and
, and 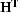 stands for the adjoint operator defined by the dot-product test
stands for the adjoint operator defined by the dot-product test
| 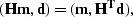 |
(244) |
where the parentheses denote the dot product:
In high-frequency asymptotics, the difference between the amplitudes
of the two inverses is simply the Jacobian term 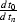 , asymptotically equal to
, asymptotically equal to 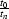 . This difference
corresponds exactly to the difference between Black's definition of
amplitude preservation Black et al. (1993) and the definition used in Born
DMO Bleistein (1990); Liner (1991), as discussed above. While operator
(
. This difference
corresponds exactly to the difference between Black's definition of
amplitude preservation Black et al. (1993) and the definition used in Born
DMO Bleistein (1990); Liner (1991), as discussed above. While operator
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) preserves amplitudes in the Born DMO sense, Ronen's
inverse satisfies Black's amplitude preservation criteria. This means
Ronen's operator implies that the ``geometric spreading'' correction
(multiplication by time) has been performed on the data prior to DMO.
) preserves amplitudes in the Born DMO sense, Ronen's
inverse satisfies Black's amplitude preservation criteria. This means
Ronen's operator implies that the ``geometric spreading'' correction
(multiplication by time) has been performed on the data prior to DMO.
To construct a one-term DMO operator, thus avoiding the estimation of
the offset derivative in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), let us consider the problem
of inverting the inverse DMO operator (
), let us consider the problem
of inverting the inverse DMO operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). One of the
possible approaches to this problem is the least-squares iterative
inversion, as proposed by Ronen 1987. This
requires constructing the adjoint operator, which is Hale's DMO (or
its analog) in the case of Ronen's method. The iterative least-squares
approach can account for irregularities in the data geometry
Ronen et al. (1991); Ronen (1994) and boundary effects, but it is computationally
expensive because of the multiple application of the operators. An
alternative approach is the asymptotic inversion, which can be viewed
as a special case of preconditioning the adjoint operator
Chemingui and Biondi (1996); Liner and Cohen (1988). The goal of the asymptotical inverse is to
reconstruct the geometry and the amplitudes of the reflection events
in the high-frequency asymptotical limit.
). One of the
possible approaches to this problem is the least-squares iterative
inversion, as proposed by Ronen 1987. This
requires constructing the adjoint operator, which is Hale's DMO (or
its analog) in the case of Ronen's method. The iterative least-squares
approach can account for irregularities in the data geometry
Ronen et al. (1991); Ronen (1994) and boundary effects, but it is computationally
expensive because of the multiple application of the operators. An
alternative approach is the asymptotic inversion, which can be viewed
as a special case of preconditioning the adjoint operator
Chemingui and Biondi (1996); Liner and Cohen (1988). The goal of the asymptotical inverse is to
reconstruct the geometry and the amplitudes of the reflection events
in the high-frequency asymptotical limit.
According to Beylkin's theory of asymptotical inversion, also known as
the generalized Radon transform Beylkin (1985), two operators of the
form
| ![\begin{displaymath}
D(\omega)=\int X(t,\omega)\,M(t)\,
\exp\left[i\omega \phi (t,\omega)\right]\,dt\end{displaymath}](img426.gif) |
(245) |
and
| ![\begin{displaymath}
\widetilde{M}(t)=\int Y(t,\omega)\,D(\omega)\,
\exp\left[-i\omega \phi (t,\omega)\right]\,d\omega\end{displaymath}](img427.gif) |
(246) |
constitute a pair of asymptotically inverse operators
(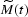 matching M(t) in the high-frequency asymptotics)
if
matching M(t) in the high-frequency asymptotics)
if
| 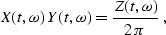 |
(247) |
where Z is the ``Beylkin determinant''
| 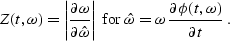 |
(248) |
With respect to the high-frequency asymptotical representation, we can
recast (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the equivalent form by moving the time
derivative under the integral sign:
) in the equivalent form by moving the time
derivative under the integral sign:
| ![\begin{displaymath}
\widetilde{P}(t_n,k) \approx
{H(t_n) \over {2\,\pi}}\,\mbox...
...p\left(-i \omega_0\,\vert t_n\vert\,A\right)
\,d\omega_0\right]\end{displaymath}](img431.gif) |
(249) |
Now the asymptotical inverse of (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is evaluated by
means of Beylkin's method (
) is evaluated by
means of Beylkin's method (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which leads
to an amplitude-preserving one-term DMO operator of the form
), which leads
to an amplitude-preserving one-term DMO operator of the form
| ![\begin{displaymath}
\widetilde{\widetilde{P}}_0(\omega_0,k) =
\mbox{Im}\left[
\...
...\exp\left(i \omega_0\,\vert t_1\vert\,A\right)
\,dt_1\right]\;,\end{displaymath}](img432.gif) |
(250) |
where
| 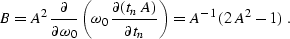 |
(251) |
The amplitude factor (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds exactly to that of
Born DMO Bleistein (1990) in full accordance with the conclusions of the
asymptotical analysis of the offset-continuation amplitudes. An
analogous result can be obtained with the different definition of
amplitude preservation proposed by Black et al. 1993. In
the time-and-space domain, the operator asymptotically analogous to
(
) corresponds exactly to that of
Born DMO Bleistein (1990) in full accordance with the conclusions of the
asymptotical analysis of the offset-continuation amplitudes. An
analogous result can be obtained with the different definition of
amplitude preservation proposed by Black et al. 1993. In
the time-and-space domain, the operator asymptotically analogous to
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is found by applying either the stationary phase
technique Black et al. (1993); Liner (1990) or Goldin's method of
discontinuities Goldin (1988, 1990), which is the
time-and-space analog of Beylkin's asymptotical inverse theory
Stovas and Fomel (1996). The time-and-space asymptotical DMO operator takes the
form
) is found by applying either the stationary phase
technique Black et al. (1993); Liner (1990) or Goldin's method of
discontinuities Goldin (1988, 1990), which is the
time-and-space analog of Beylkin's asymptotical inverse theory
Stovas and Fomel (1996). The time-and-space asymptotical DMO operator takes the
form
| 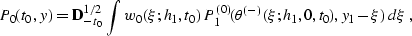 |
(252) |
where the weighting function w0 is defined as
| 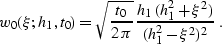 |
(253) |





Next: Offset continuation in the
Up: Offset continuation for reflection
Previous: The Cauchy problem and
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
) with the Fourier-domain DMO operators, which
have been the standard for DMO processing since Hale's outstanding
work Hale (1983, 1984).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in
Appendix
) in
Appendix ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and setting the output offset to zero,
we obtain the following DMO-like integral operators in the t-k
domain:
and setting the output offset to zero,
we obtain the following DMO-like integral operators in the t-k
domain:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to the time variable
t0 reduces to known integrals Gradshtein and Ryzhik (1994) and creates explicit
DMO-type operators in the frequency-wavenumber domain, as follows:
) with respect to the time variable
t0 reduces to known integrals Gradshtein and Ryzhik (1994) and creates explicit
DMO-type operators in the frequency-wavenumber domain, as follows:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) coincides exactly with the imaginary part
of Hale's DMO operator Hale (1984). However, unlike Hale's,
operator (
) coincides exactly with the imaginary part
of Hale's DMO operator Hale (1984). However, unlike Hale's,
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is causal, which means that its impulse
response does not continue to negative times. The non-causality of
Hale's DMO and related issues are discussed in more detail by
Stovas and Fomel (1996) and Fomel (1995b).
) is causal, which means that its impulse
response does not continue to negative times. The non-causality of
Hale's DMO and related issues are discussed in more detail by
Stovas and Fomel (1996) and Fomel (1995b).
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which transforms to the second term in the DMO
operator (
), which transforms to the second term in the DMO
operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Note that this term vanishes at the input offset
equal to zero, which represents the case of the inverse DMO operator.
). Note that this term vanishes at the input offset
equal to zero, which represents the case of the inverse DMO operator.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as
) as
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with respect to the time
variable t0 according to equation (
) with respect to the time
variable t0 according to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we get the
Fourier-domain version of the ``amplitude-preserving'' inverse DMO:
), we get the
Fourier-domain version of the ``amplitude-preserving'' inverse DMO:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) with Ronen's version of inverse DMO
Ronen (1987), one can see that if Hale's DMO is denoted
by
) with Ronen's version of inverse DMO
Ronen (1987), one can see that if Hale's DMO is denoted
by ![]() , then Ronen's inverse DMO is
, then Ronen's inverse DMO is ![]() , while the amplitude-preserving inverse (
, while the amplitude-preserving inverse (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
is
)
is ![]() . Here
. Here ![]() is the derivative
operator
is the derivative
operator ![]() , and
, and ![]() stands for the adjoint operator defined by the dot-product test
stands for the adjoint operator defined by the dot-product test
![]() , asymptotically equal to
, asymptotically equal to ![]() . This difference
corresponds exactly to the difference between Black's definition of
amplitude preservation Black et al. (1993) and the definition used in Born
DMO Bleistein (1990); Liner (1991), as discussed above. While operator
(
. This difference
corresponds exactly to the difference between Black's definition of
amplitude preservation Black et al. (1993) and the definition used in Born
DMO Bleistein (1990); Liner (1991), as discussed above. While operator
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) preserves amplitudes in the Born DMO sense, Ronen's
inverse satisfies Black's amplitude preservation criteria. This means
Ronen's operator implies that the ``geometric spreading'' correction
(multiplication by time) has been performed on the data prior to DMO.
) preserves amplitudes in the Born DMO sense, Ronen's
inverse satisfies Black's amplitude preservation criteria. This means
Ronen's operator implies that the ``geometric spreading'' correction
(multiplication by time) has been performed on the data prior to DMO.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), let us consider the problem
of inverting the inverse DMO operator (
), let us consider the problem
of inverting the inverse DMO operator (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). One of the
possible approaches to this problem is the least-squares iterative
inversion, as proposed by Ronen 1987. This
requires constructing the adjoint operator, which is Hale's DMO (or
its analog) in the case of Ronen's method. The iterative least-squares
approach can account for irregularities in the data geometry
Ronen et al. (1991); Ronen (1994) and boundary effects, but it is computationally
expensive because of the multiple application of the operators. An
alternative approach is the asymptotic inversion, which can be viewed
as a special case of preconditioning the adjoint operator
Chemingui and Biondi (1996); Liner and Cohen (1988). The goal of the asymptotical inverse is to
reconstruct the geometry and the amplitudes of the reflection events
in the high-frequency asymptotical limit.
). One of the
possible approaches to this problem is the least-squares iterative
inversion, as proposed by Ronen 1987. This
requires constructing the adjoint operator, which is Hale's DMO (or
its analog) in the case of Ronen's method. The iterative least-squares
approach can account for irregularities in the data geometry
Ronen et al. (1991); Ronen (1994) and boundary effects, but it is computationally
expensive because of the multiple application of the operators. An
alternative approach is the asymptotic inversion, which can be viewed
as a special case of preconditioning the adjoint operator
Chemingui and Biondi (1996); Liner and Cohen (1988). The goal of the asymptotical inverse is to
reconstruct the geometry and the amplitudes of the reflection events
in the high-frequency asymptotical limit.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in the equivalent form by moving the time
derivative under the integral sign:
) in the equivalent form by moving the time
derivative under the integral sign:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is evaluated by
means of Beylkin's method (
) is evaluated by
means of Beylkin's method (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )-(
)-(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), which leads
to an amplitude-preserving one-term DMO operator of the form
), which leads
to an amplitude-preserving one-term DMO operator of the form
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) corresponds exactly to that of
Born DMO Bleistein (1990) in full accordance with the conclusions of the
asymptotical analysis of the offset-continuation amplitudes. An
analogous result can be obtained with the different definition of
amplitude preservation proposed by Black et al. 1993. In
the time-and-space domain, the operator asymptotically analogous to
(
) corresponds exactly to that of
Born DMO Bleistein (1990) in full accordance with the conclusions of the
asymptotical analysis of the offset-continuation amplitudes. An
analogous result can be obtained with the different definition of
amplitude preservation proposed by Black et al. 1993. In
the time-and-space domain, the operator asymptotically analogous to
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is found by applying either the stationary phase
technique Black et al. (1993); Liner (1990) or Goldin's method of
discontinuities Goldin (1988, 1990), which is the
time-and-space analog of Beylkin's asymptotical inverse theory
Stovas and Fomel (1996). The time-and-space asymptotical DMO operator takes the
form
) is found by applying either the stationary phase
technique Black et al. (1993); Liner (1990) or Goldin's method of
discontinuities Goldin (1988, 1990), which is the
time-and-space analog of Beylkin's asymptotical inverse theory
Stovas and Fomel (1996). The time-and-space asymptotical DMO operator takes the
form