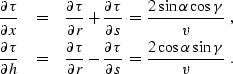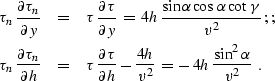Next: Offset continuation geometry: time
Up: Introducing the offset continuation
Previous: Proof of kinematic equivalence
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and the previously published OC
equation Bolondi et al. (1982) differ only with respect to the
single term
) and the previously published OC
equation Bolondi et al. (1982) differ only with respect to the
single term 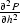 . However, this
difference is substantial.
. However, this
difference is substantial.
From the offset continuation characteristic equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can conclude that the first-order traveltime
derivative with respect to offset decreases with a decrease of the
offset. At zero offset the derivative equals zero, as predicted by the
principle of reciprocity (the reflection traveltime has to be an
even function of offset). Neglecting
), we can conclude that the first-order traveltime
derivative with respect to offset decreases with a decrease of the
offset. At zero offset the derivative equals zero, as predicted by the
principle of reciprocity (the reflection traveltime has to be an
even function of offset). Neglecting 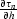 in (
in (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) leads to the characteristic
equation
) leads to the characteristic
equation
| 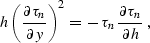 |
(152) |
which corresponds to the approximate OC equation of
Bolondi et al. (1982). The approximate equation has the form
| 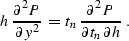 |
(153) |
Comparing (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), note that
approximation (
), note that
approximation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is valid only if
) is valid only if
| 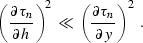 |
(154) |
To find the geometric constraints implied by inequality
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can express the traveltime derivatives in
geometric terms. As follows from expressions (
), we can express the traveltime derivatives in
geometric terms. As follows from expressions (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and
(
) and
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
),
| 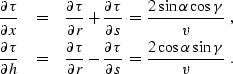 |
(155) |
| (156) |
Expression (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) allows transforming
equations (
) allows transforming
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the form
) to the form
| 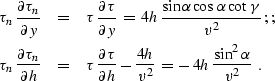 |
(157) |
| (158) |
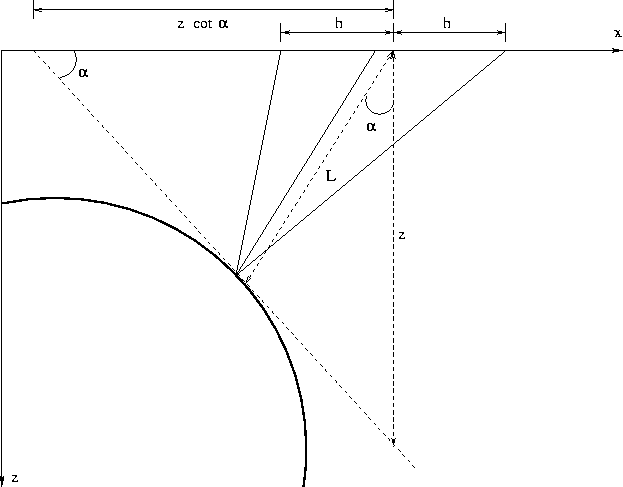
Without loss of generality, we can assume  to be positive.
Consider a plane tangent to a true reflector at the reflection
point
(Figure
to be positive.
Consider a plane tangent to a true reflector at the reflection
point
(Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The traveltime of a wave, reflected from the plane, has the
well-known explicit expression
).
The traveltime of a wave, reflected from the plane, has the
well-known explicit expression
| 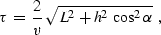 |
(159) |
where L is the length of the normal ray from the midpoint. As
follows from combining (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) and (
) and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
),
| 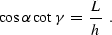 |
(160) |
We can then combine equalities (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ),
(
),
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), and (
), and (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to transform
inequality (
) to transform
inequality (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) to the form
) to the form
| 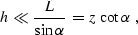 |
(161) |
where z is the depth of the plane reflector under the midpoint. For
example, for a dip of 45 degrees, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is
satisfied only for offsets that are much smaller than the depth.
) is
satisfied only for offsets that are much smaller than the depth.
ocobol
Figure 3 Reflection rays and
tangent to the reflector in a constant velocity medium (a scheme).
|
|  |






Next: Offset continuation geometry: time
Up: Introducing the offset continuation
Previous: Proof of kinematic equivalence
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we can conclude that the first-order traveltime
derivative with respect to offset decreases with a decrease of the
offset. At zero offset the derivative equals zero, as predicted by the
principle of reciprocity (the reflection traveltime has to be an
even function of offset). Neglecting
), we can conclude that the first-order traveltime
derivative with respect to offset decreases with a decrease of the
offset. At zero offset the derivative equals zero, as predicted by the
principle of reciprocity (the reflection traveltime has to be an
even function of offset). Neglecting ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) leads to the characteristic
equation
) leads to the characteristic
equation