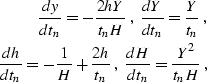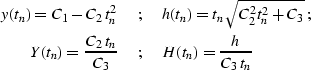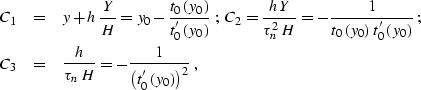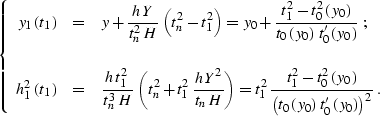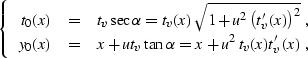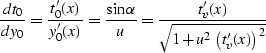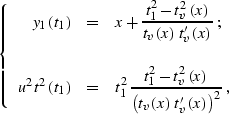Next: Proof of amplitude equivalence
Up: Introducing the offset continuation
Previous: Comparison with Bolondi's OC
To study the laws of traveltime curve transformation in the OC
process, it is convenient to apply the method of characteristics
Courant (1962) to the eikonal-type equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
characteristics of equation (
). The
characteristics of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) [
bi-characteristics with respect to equation (
) [
bi-characteristics with respect to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
are the trajectories of the high-frequency energy propagation in the
imaginary OC process. Following the formal analogy with seismic rays,
I call those trajectories time rays, where the word time
refers to the fact that the trajectories describe the traveltime
transformation Fomel (1994). According to the theory of first-order
partial differential equations, time rays are determined by a set of
ordinary differential equations (characteristic equations) derived
from equation (
)]
are the trajectories of the high-frequency energy propagation in the
imaginary OC process. Following the formal analogy with seismic rays,
I call those trajectories time rays, where the word time
refers to the fact that the trajectories describe the traveltime
transformation Fomel (1994). According to the theory of first-order
partial differential equations, time rays are determined by a set of
ordinary differential equations (characteristic equations) derived
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) :
) :
| 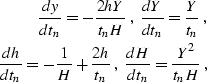 |
|
| (162) |
where Y corresponds to 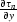 along a
ray and H corresponds to
along a
ray and H corresponds to 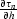 . In this
notation, equation (
. In this
notation, equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) takes the form
) takes the form
| 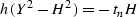 |
(163) |
and serves as an additional constraint for the definition of time
rays. System (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) can be solved by standard mathematical
methods Tenenbaum and Pollard (1985). Its general solution takes the parametric form,
where the time variable tn is the parameter changing along a time
ray:
) can be solved by standard mathematical
methods Tenenbaum and Pollard (1985). Its general solution takes the parametric form,
where the time variable tn is the parameter changing along a time
ray:
| 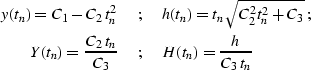 |
(164) |
| (165) |
and C1, C2, and C3 are independent coefficients, constant
along each time ray. To determine the values of these coefficients,
we can pose an initial-value (Cauchy) problem for the system of
differential equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The traveltime curve
). The traveltime curve
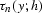 for a given common offset h and the first partial
derivative
for a given common offset h and the first partial
derivative 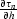 along the same constant
offset section provide natural initial conditions for the Cauchy
problem. A particular case of those conditions is the zero-offset
traveltime curve. If the first partial derivative of traveltime with
respect to offset is continuous, it vanishes at zero offset according
to the reciprocity principle (traveltime must be an even function of
the offset):
along the same constant
offset section provide natural initial conditions for the Cauchy
problem. A particular case of those conditions is the zero-offset
traveltime curve. If the first partial derivative of traveltime with
respect to offset is continuous, it vanishes at zero offset according
to the reciprocity principle (traveltime must be an even function of
the offset):
| 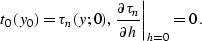 |
(166) |
Applying the initial-value conditions to the general
solution (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) generates the following expressions for the
ray invariants:
) generates the following expressions for the
ray invariants:
| 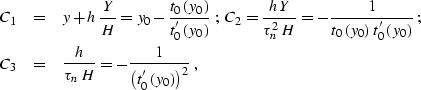 |
|
| (167) |
where 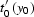 denotes the derivative
denotes the derivative
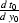 . Finally, substituting (
. Finally, substituting (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
into (
)
into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we obtain an explicit parametric form of the ray
trajectories:
), we obtain an explicit parametric form of the ray
trajectories:
| 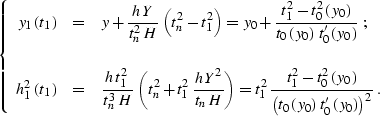 |
(168) |
Here y1, h1, and t1 are the coordinates of the continued
seismic section. The first of equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) indicates
that the time ray projections to a common-offset section have a
parabolic form. Time rays do not exist for
) indicates
that the time ray projections to a common-offset section have a
parabolic form. Time rays do not exist for 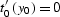 (a
locally horizontal reflector) because in this case post-NMO offset
continuation transform is not required.
(a
locally horizontal reflector) because in this case post-NMO offset
continuation transform is not required.
The actual parameter that
determines a particular time ray is the reflection point location.
This important conclusion follows from the known parametric equations
| 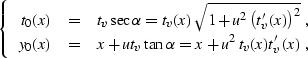 |
(169) |
where x is the reflection point, u is half of the wave velocity (u=v/2),
tv is the vertical time (reflector depth divided by u), and
 is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
is the
local reflector dip. Taking into account that the derivative of the zero-offset
traveltime curve is
| 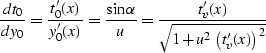 |
(170) |
and substituting (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) into (
) into (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), we get
), we get
| 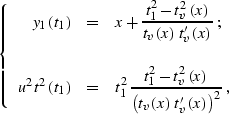 |
(171) |
where 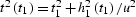 .
.
To visualize the concept of time rays, let us consider some simple
analytic examples of its application to geometric analysis of the
offset-continuation process.
The simplest and most important example is the case of a plane dipping
reflector. Putting the origin of the y axis at the intersection of
the reflector plane with the surface, we can express the reflection
traveltime after NMO in the form
| 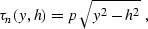 |
(172) |
where 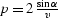 , and
, and  is the dip angle.
The zero-offset traveltime in this case is a straight line:
is the dip angle.
The zero-offset traveltime in this case is a straight line:
| 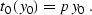 |
(173) |
According to equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), the time rays in this case
are defined by
), the time rays in this case
are defined by
| 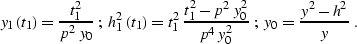 |
(174) |
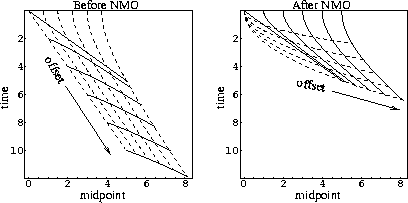
The geometry of the OC transformation is shown in Figure
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) .
ocopln
.
ocopln
Figure 4 Transformation of
the reflection traveltime curves in the OC process: the case of a
plane dipping reflector. Left: Time coordinate before the NMO
correction. Right: Time coordinate after NMO. The solid lines
indicate traveltime curves at different common-offset sections; the
dashed lines indicate time rays.

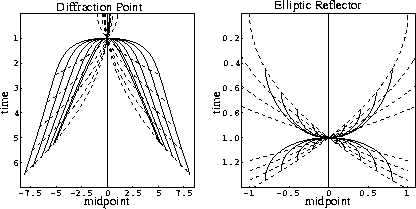
The second example is the case of a point diffractor (the left side
of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). Without loss of generality, the origin
of the midpoint axis can be put above the diffraction point. In this
case the zero-offset reflection traveltime curve has the well-known
hyperbolic form
). Without loss of generality, the origin
of the midpoint axis can be put above the diffraction point. In this
case the zero-offset reflection traveltime curve has the well-known
hyperbolic form
| 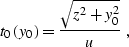 |
(175) |
where z is the depth of the diffractor and u=v/2 is half of the
wave velocity. Time rays are defined according to
equations (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), as follows:
), as follows:
| 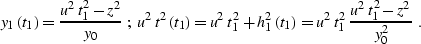 |
(176) |
ococrv
Figure 5 Transformation of
the reflection traveltime curves in the OC process. Left: the case
of a diffraction point. Right: the case of an elliptic reflector.
Solid lines indicate traveltime curves at different common-offset
sections, dashed lines indicate time rays.

The third example (the right side of Figure ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the
curious case of a focusing elliptic reflector. Let y be the center
of the ellipse and h be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
Deregowski and Rocca (1981):
) is the
curious case of a focusing elliptic reflector. Let y be the center
of the ellipse and h be half the distance between the foci of the
ellipse. If both foci are on the surface, the zero-offset
traveltime curve is defined by the so-called ``DMO smile''
Deregowski and Rocca (1981):
| 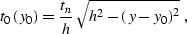 |
(177) |
where 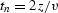 , and z is the small semi-axis of the ellipse.
The time-ray equations are
, and z is the small semi-axis of the ellipse.
The time-ray equations are
| 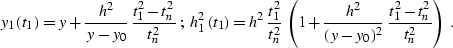 |
(178) |
When y1 coincides with y, and h1 coincides with h, the
source and the receiver are in the foci of the elliptic reflector, and
the traveltime curve degenerates to a point t1=tn. This remarkable
fact is the actual basis of the geometric theory of dip moveout
Deregowski and Rocca (1981).





Next: Proof of amplitude equivalence
Up: Introducing the offset continuation
Previous: Comparison with Bolondi's OC
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). The
characteristics of equation (
). The
characteristics of equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) [
bi-characteristics with respect to equation (
) [
bi-characteristics with respect to equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )]
are the trajectories of the high-frequency energy propagation in the
imaginary OC process. Following the formal analogy with seismic rays,
I call those trajectories time rays, where the word time
refers to the fact that the trajectories describe the traveltime
transformation Fomel (1994). According to the theory of first-order
partial differential equations, time rays are determined by a set of
ordinary differential equations (characteristic equations) derived
from equation (
)]
are the trajectories of the high-frequency energy propagation in the
imaginary OC process. Following the formal analogy with seismic rays,
I call those trajectories time rays, where the word time
refers to the fact that the trajectories describe the traveltime
transformation Fomel (1994). According to the theory of first-order
partial differential equations, time rays are determined by a set of
ordinary differential equations (characteristic equations) derived
from equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) :
) :