




Next: Proof of kinematic equivalence
Up: Introducing the offset continuation
Previous: Introducing the offset continuation
A simplified version of the ray method technique Babich (1991); Cerveny et al. (1977)
can allow us to prove the theoretical validity of
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for all offsets and reflector dips by
deriving two equations that describe separately wavefront (traveltime)
and amplitude transformation. According to the formal ray theory,
the leading term of the high-frequency asymptotics for a reflected
wave recorded on a seismogram takes the form
) for all offsets and reflector dips by
deriving two equations that describe separately wavefront (traveltime)
and amplitude transformation. According to the formal ray theory,
the leading term of the high-frequency asymptotics for a reflected
wave recorded on a seismogram takes the form
| 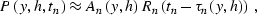 |
(142) |
where An stands for the amplitude, Rn is the wavelet shape of
the leading high-frequency term, and 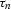 is the traveltime curve
after normal moveout. Inserting (
is the traveltime curve
after normal moveout. Inserting (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) as a trial
solution for (
) as a trial
solution for (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ), collecting terms that have the
same asymptotic order (correspond to the same-order derivatives of the
wavelet Rn), and neglecting low-order terms, we obtain a set of two
first-order partial differential equations:
), collecting terms that have the
same asymptotic order (correspond to the same-order derivatives of the
wavelet Rn), and neglecting low-order terms, we obtain a set of two
first-order partial differential equations:
| 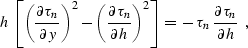 |
(143) |
| 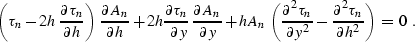 |
(144) |
Equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) describes the transformation of
traveltime curve geometry in the OC process analogously to how the
eikonal equation describes the front propagation in the classic wave
theory. What appear to be wavefronts of the wave motion described by
equation (
) describes the transformation of
traveltime curve geometry in the OC process analogously to how the
eikonal equation describes the front propagation in the classic wave
theory. What appear to be wavefronts of the wave motion described by
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) are traveltime curves of reflected
waves recorded on seismic sections. The law of amplitude
transformation for high-frequency wave components related to those
wavefronts is given by equation (
) are traveltime curves of reflected
waves recorded on seismic sections. The law of amplitude
transformation for high-frequency wave components related to those
wavefronts is given by equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). In terms of
the theory of partial differential equations,
equation (
). In terms of
the theory of partial differential equations,
equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) is the characteristic equation
for (
) is the characteristic equation
for (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
).





Next: Proof of kinematic equivalence
Up: Introducing the offset continuation
Previous: Introducing the offset continuation
Stanford Exploration Project
12/28/2000
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) for all offsets and reflector dips by
deriving two equations that describe separately wavefront (traveltime)
and amplitude transformation. According to the formal ray theory,
the leading term of the high-frequency asymptotics for a reflected
wave recorded on a seismogram takes the form
) for all offsets and reflector dips by
deriving two equations that describe separately wavefront (traveltime)
and amplitude transformation. According to the formal ray theory,
the leading term of the high-frequency asymptotics for a reflected
wave recorded on a seismogram takes the form