|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
One difficulty for heterogeneous grains comes from the additional constant ![]() that I do not know how to determine independently from the other poroelastic measurements.
But this fundamental problem is actually no different for the anisotropic case than it was for
the isotropic one, and the solution is also the same. In both cases, I need more information,
and in both cases the necessary information will most likely come
from our knowledge of the Skempton (1954) coefficient
that I do not know how to determine independently from the other poroelastic measurements.
But this fundamental problem is actually no different for the anisotropic case than it was for
the isotropic one, and the solution is also the same. In both cases, I need more information,
and in both cases the necessary information will most likely come
from our knowledge of the Skempton (1954) coefficient ![]() .
If I assume that
.
If I assume that ![]() can be directly measured (which is plausible, since
can be directly measured (which is plausible, since
![]() in the undrained case
when a uniform confining pressure is applied to the system), then the problem is completely solved,
because
in the undrained case
when a uniform confining pressure is applied to the system), then the problem is completely solved,
because ![]() is the key to solving for the coefficients
is the key to solving for the coefficients ![]() in (48).
The only new difficulty is that the terms of the form
in (48).
The only new difficulty is that the terms of the form 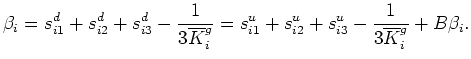 must also be replaced by
the partial grain compliance sums
must also be replaced by
the partial grain compliance sums
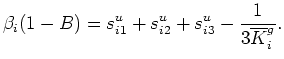 , as shown in (30). So I now have
, as shown in (30). So I now have
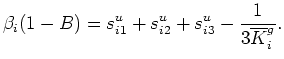 , or to find some
way of avoiding the necessity of doing so.
, or to find some
way of avoiding the necessity of doing so.
In principle, this can be done experimentally by actually performing a test on the porous
sample that applies the same pressure inside and outside. Then, measurements of the change in
strain in the three orthogonal directions ![]() would provide direct measures of the
quantities
would provide direct measures of the
quantities
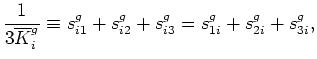 needed. So this approach is one that is experimentally feasible.
needed. So this approach is one that is experimentally feasible.
An alternative that I have not considered so far would be to perform shear tests
by applying nonzero deviatoric stress changes (Lockner and Stanchits, 2002; Skempton, 1954). The undrained fluid pressure
is given by
![]() , where the mean stress is
, where the mean stress is
![]() .
But, if the
.
But, if the
![]() 's are not uniform, then there are also deviatoric
stresses present, due to the nonuniformity of the principal stresses.
's are not uniform, then there are also deviatoric
stresses present, due to the nonuniformity of the principal stresses.
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |