|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
The matrix in (22) is in compliance form and
has extremely simple poroelastic behavior in the sense
that all the fluid mechanical effects
appear only in the single coefficient 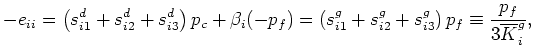 . I can simplify the
notation a little more by lumping some coefficients together,
combining the
. I can simplify the
notation a little more by lumping some coefficients together,
combining the 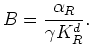 submatrix in the upper left corner of the matrix
in (22) as
submatrix in the upper left corner of the matrix
in (22) as ![]() , and defining the column vector
, and defining the column vector ![]() by
by
The resulting ![]() matrix and its inverse are now related by:
matrix and its inverse are now related by:
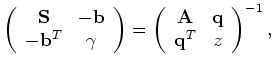 by introducing three components: (a) scalar
by introducing three components: (a) scalar
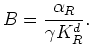 stiffness matrix (i.e., the
pertinent one connecting the principal strains to principal stresses)
stiffness matrix (i.e., the
pertinent one connecting the principal strains to principal stresses)
Also, note the important fact that the observed decoupling of the fluid effects occurs only in the compliance form (22) of the equations, and never in the stiffness (inverse) form for the poroelasticity equations.
From these results, it is not hard to show that
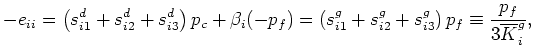 , together with the three distinct orthotropic
, together with the three distinct orthotropic
renewedcommandarraystretch1.2
par
begincenter
sc Table 1. Reuss (R), Voigt (V), and self-consistent effective (![]() )
bulk moduli of various common anisotropic materials cite[]berryman05:
Water ice, cadmium, zinc, graphite,
)
bulk moduli of various common anisotropic materials cite[]berryman05:
Water ice, cadmium, zinc, graphite,
![]() -quartz, corundum,
barium titanate, rutile,
aluminum, copper, magnesia, spinel.
Full references for the data used in both sc Tables 1 and 2 are provided
in citeberryman05. Units of bulk modulus
-quartz, corundum,
barium titanate, rutile,
aluminum, copper, magnesia, spinel.
Full references for the data used in both sc Tables 1 and 2 are provided
in citeberryman05. Units of bulk modulus ![]() are GPa.
are GPa.
par
begintabular|c|c|c|c|c|c| hlinehline
Material & Symmetry & ![]() &
& ![]() &
& ![]() &
& ![]()
hline
H![]() O & Hexagonal & 8.89 & 8.89 & 8.89 & 1.00
O & Hexagonal & 8.89 & 8.89 & 8.89 & 1.00
Cd & Hexagonal & 48.8 & 54.7 & 58.1 & 1.19
Zn & Hexagonal & 61.6 & 70.9 & 75.1 & 1.22
Graphite & Hexagonal & 35.8 & 88.0 & 286.3 & 8.00
hline
Al![]() O
O![]() & Trigonal & 253.5 & 253.7 & 253.9 & 1.002
& Trigonal & 253.5 & 253.7 & 253.9 & 1.002
![]() -SiO
-SiO![]() & Trigonal & 37.6 & 37.8 & 38.1 & 1.01
& Trigonal & 37.6 & 37.8 & 38.1 & 1.01
hline
TiO![]() & Tetragonal & 209 & 213 & 218 & 1.04
& Tetragonal & 209 & 213 & 218 & 1.04
BaTiO![]() & Tetragonal & 163.1 & 179.3 & 186.8 & 1.15
& Tetragonal & 163.1 & 179.3 & 186.8 & 1.15
hline
Al & Cubic & 76.3 & 76.3 & 76.3 & 1.00
MgO & Cubic & 162.4 & 162.4 & 162.4 & 1.00
MgAl![]() O
O![]() & Cubic & 196.7 & 196.7 & 196.7 & 1.00
& Cubic & 196.7 & 196.7 & 196.7 & 1.00
Cu & Cubic & 138.0 & 138.0 & 138.0 & 1.00
hlinehline
endtabular
endcenter
par
subsectionDeducing coefficients from measurements: Anisotropic example with homogeneous grains
par
Now, further progress is made by considering the Reuss average again for both of the orthotropic
drained and undrained compliances:
beginequation
frac1K_R^d equiv sum_i,j = 1,2,3 s^d_ij,
labeleq:drainedKR
endequation
and
beginequation
frac1K_R^u equiv sum_i,j = 1,2,3 s^u_ij.
labeleq:undrainedKR
endequation
These effective moduli are the Reuss averages of the nine compliances in the upper left
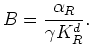 of the full (including the uncoupled shear components)
of the full (including the uncoupled shear components)
![]() compliance matrix for the two cases, respectively, when the pore fluid is allowed
to drain from the porous system, and when the pore fluid is trapped by a jacketing
material and therefore undrained.
par
1.2
compliance matrix for the two cases, respectively, when the pore fluid is allowed
to drain from the porous system, and when the pore fluid is trapped by a jacketing
material and therefore undrained.
par
1.2
| Material | Symmetry | |
||||
| H |
Hexagonal | 3.48 | 3.52 | 3.55 | 1.02 | 0.10 |
| Cd | Hexagonal | 22.1 | 24.3 | 26.4 | 1.19 | 1.14 |
| Zn | Hexagonal | 34.1 | 40.6 | 44.8 | 1.31 | 1.77 |
| Graphite | Hexagonal | 9.2 | 52.6 | 219.4 | 23.8 | 121.0 |
|
Al |
Trigonal | 160.7 | 163.1 | 165.5 | 1.03 | 0.15 |
| Trigonal | 41.0 | 44.0 | 47.6 | 1.16 | 0.81 | |
|
TiO |
Tetragonal | 99.5 | 114.5 | 124.9 | 1.26 | 1.34 |
| BaTiO |
Tetragonal | 47.4 | 53.6 | 59.8 | 1.26 | 1.46 |
| Al | Cubic | 26.0 | 26.2 | 26.3 | 1.01 | 0.05 |
| MgO | Cubic | 123.9 | 126.3 | 128.6 | 1.04 | 0.20 |
| MgAl |
Cubic | 98.6 | 109.0 | 118.0 | 1.20 | 1.00 |
| Cu | Cubic | 40.0 | 46.3 | 51.3 | 1.28 | 1.41 |
Although the significance of the formula in the anisotropic case is somewhat different now, I find again that
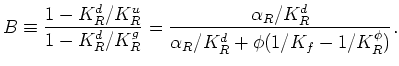 is not an approximation.
In fact it is important now in the anisotropic case (but not in the isotropic cases considered earlier
as long as the grains were also homogeneous) to make this distinction between the Reuss and Voigt averages.
Making this choice of notation will help demonstrate useful analogies between the rigorous
anisotropic formulas and the isotropic ones. I have prepared the way for these analogies
by using the Reuss averages in earlier notation, even though they were mostly redundant
in those isotropic examples.
is not an approximation.
In fact it is important now in the anisotropic case (but not in the isotropic cases considered earlier
as long as the grains were also homogeneous) to make this distinction between the Reuss and Voigt averages.
Making this choice of notation will help demonstrate useful analogies between the rigorous
anisotropic formulas and the isotropic ones. I have prepared the way for these analogies
by using the Reuss averages in earlier notation, even though they were mostly redundant
in those isotropic examples.
First note that, from (42) and (44),
it follows that
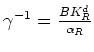 -- also see (36).
So I can now rearrange (39) to give the formal relationship
-- also see (36).
So I can now rearrange (39) to give the formal relationship
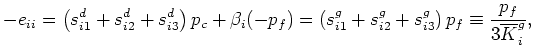 are now precisely determined. All the remaining drained compliances
are now precisely determined. All the remaining drained compliances
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |