Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media

Deducing anisotropic drained constants from undrained: Homogeneous grains and pores

I am now in position to develop the analogy between the isotropic and anisotropic Gassmann (1951) equations for the case of homogeneous grains. In particular, the equation for the suspension modulus in (2) does not change at all. In contrast, the equation for the effective undrained bulk modulus $K^u$, as shown in both (1) and (3), changes only in that the relationship is now between the Reuss averages $K_R^u$ and $K_R^d$ of these quantities. This result is completely analogous to (3), and so will not be shown here.

Since the remainder of the argument is virtually identical to the isotropic case, I therefore obtain:

$$K_R^d = \left(\frac{K_R^u}{K_{susp}} - 1\right)\left[1/K_{susp} - 2/K_R^g + K_R^u/(K_R^g)^2\right]^{-1}.$$ (47)

This formula shows how to invert for drained Reuss bulk modulus $K_R^d$ from knowledge of $K_R^u$, $\phi$, $K_f$ and $K_R^g$ in an anisotropic (up to orthotropic) poroelastic system.

1.2

TABLE 3.for the principal stiffness coefficients $c_{ij}$ of orthorhombic sulfur (S), Rochelle salt, Benzophenone, and $alpha$-Uranium ($alpha$-U). All data from Musgrave (2003), but re-expressed in units of GPa.

Stiffness	Sulfur (S)	Rochelle Salt	Benzophenone	$alpha$-Uranium
$c_{11}$	24.0	25.5	107.0	215.0
$c_{22}$	20.5	38.1	100.0	199.0
$c_{33}$	48.3	37.1	71.0	267.0
$c_{12}$	13.3	14.1	55.0	46.0
$c_{13}$	17.1	11.6	16.9	22.0
$c_{23}$	15.9	14.6	32.1	107.0

1.2

TABLE 4.for various measures of bulk modulus $K$ (Voigt, Reuss, and three partial sum moduli) for orthorhombic sulfur (S), Rochelle salt, Benzophenone, and $alpha$-Uranium ($alpha$-U). All data from Musgrave (2003) [see TABLE 3 here], while the expressions in the main text were used for the computations. All moduli in units of GPa.

Bulk Modulus	Sulfur (S)	Rochelle Salt	Benzophenone	$alpha$-Uranium
$K_V$	20.6	20.1	54.0	114.6
$K_R$	17.6	19.3	49.2	111.3
$K_1$	15.2	12.5	55.8	87.9
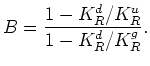$K_2$	10.1	30.6	107.5	113.6
$K_3$	15.8	23.3	29.6	147.7

Clearly this formula does not yet provide the individual compliance matrix elements $s_{ij}^d$ directly. Nevertheless, Equation (49) was the hardest step in the overall procedure. The rest of the steps follow easily once I have this rigorous result available to use.

To finish the analysis, I make use of the newly computed value of $K_R^d$, and substitute this number into the formula for $B$, which in this case is:

$$B = \frac{1-K_R^d/K_R^u}{1-K_R^d/K_R^g}.$$ (48)

Once I know Skempton coefficient $B$, this value can be substituted into (48) in order to determine the $\beta_i$ coefficients for $i = 1,2,3$. The remaining coefficient is $\gamma = \alpha_R/BK_R^d$. So I have shown that the critical step in this process was determining the value of the drained Reuss bulk modulus $K_R^d$.

Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media