 |
 |
 |
 | Poroelastic measurements resulting in complete data sets for granular
and other anisotropic porous media |  |
![[pdf]](icons/pdf.png) |
Next: Heterogeneous grains
Up: ISOTROPIC POROELASTICITY
Previous: Homogeneous grains
Rewriting Gassmann's formula in these terms, I first find that
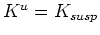 |
(3) |
Note that all explicit porosity (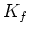 ) dependence is now imbedded in the
modulus
) dependence is now imbedded in the
modulus 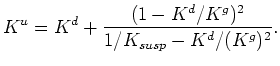 . Now if I simply multiply through by the denominator
on the right hand side, then I find
. Now if I simply multiply through by the denominator
on the right hand side, then I find
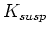 |
(4) |
Also notice that two terms of the form
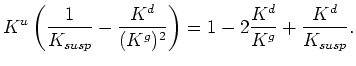 have cancelled from this expression.
Once these convenient cancellations have occurred,
have cancelled from this expression.
Once these convenient cancellations have occurred, 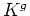 appears only linearly in the resulting expression.
The equation can therefore be solved immediately for drained modulus
appears only linearly in the resulting expression.
The equation can therefore be solved immediately for drained modulus 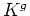 in terms of
the undrained modulus
in terms of
the undrained modulus 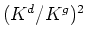 and the other factors that are also assumed to be known (and in fact
these other factors are usually easier to measure than either
and the other factors that are also assumed to be known (and in fact
these other factors are usually easier to measure than either 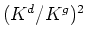 or
or 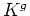 ). Finally, I obtain:
). Finally, I obtain:
![$\displaystyle K^d = \left(\frac{K^u}{K_{susp}} - 1\right)\left[1/K_{susp} - 2/K^g + K^u/(K^g)^2\right]^{-1}.$](img16.png) |
(5) |
This result shows that the drained modulus can be deduced from measurements of the undrained
modulus, together with knowledge of 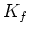 ,
, 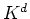 , and
, and 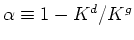 . Note that this result was first derived
by Zhu and McMechan (1990), but apparently published only in an SEG conference proceedings.
. Note that this result was first derived
by Zhu and McMechan (1990), but apparently published only in an SEG conference proceedings.
 |
 |
 |
 | Poroelastic measurements resulting in complete data sets for granular
and other anisotropic porous media |  |
![[pdf]](icons/pdf.png) |
Next: Heterogeneous grains
Up: ISOTROPIC POROELASTICITY
Previous: Homogeneous grains
2009-10-19
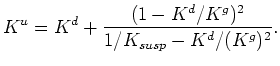 . Now if I simply multiply through by the denominator
on the right hand side, then I find
. Now if I simply multiply through by the denominator
on the right hand side, then I find
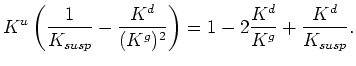 have cancelled from this expression.
Once these convenient cancellations have occurred,
have cancelled from this expression.
Once these convenient cancellations have occurred,