Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media

Homogeneous grains

The famous equation for undrained bulk modulus named for Gassmann (1951) can be written in the form

$$K^u = K^d + \alpha^2/[(\alpha-\phi)/K^g + \phi/K_f]$$ (1)

for isotropic systems, where $\alpha \equiv 1 - K^d/K^g$ is the Biot-Willis coefficient or effective stress (Biot and Willis, 1957) coefficient, $K^g$ is the solid modulus of the grains (assumed homogeneous), $K^d$ is the drained modulus of the porous medium, $K_f$ is the pore fluid modulus, and $\phi$ is the porosity. The formula becomes more complicated if the solids constituting the porous medium are heterogeneous. But we will delay discussion of this point to the next subsection and for now assume that the solids are truly homogeneous. For notational convenience, I next introduce a modulus for a fluid suspension having the same solid and fluid components as well as the same porosity, but having drained modulus $K^d \equiv 0$. Then I find that the effective modulus is given by

$$K_{susp} = \left[\frac{1-\phi}{K^g} + \frac{\phi}{K_f}\right]^{-1}.$$ (2)

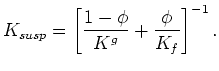In fact this result follows directly from Gassmann's formula (1) by setting $K^d = 0$ everywhere, since then $K^u = K_{susp}$. But of course this result is also well-known in mechanics and acoustics (Wood, 1955) for these types of fluid-solid suspensions.

Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media