|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |
One common example of this type of measurement uses triaxial testing [see Lockner and Stanchits (2002)],
where a two-sided confining stress is defined as
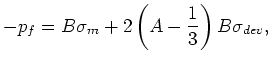 ,
and then the deviatoric stress is determined by
,
and then the deviatoric stress is determined by
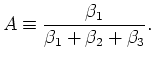 of Skempton (1954).
of Skempton (1954).
1.2
| Stiffness | Cadmium (Cd) | H |
Titanium (Ti) | Zirconium (Zr) | |
| 115.30 | 13.85 | 116.6 | 163.9 | 137.0 | |
| 51.20 | 14.99 | 110.4 | 181.6 | 160.7 | |
| 39.24 | 7.07 | 16.7 | 91.3 | 75.6 | |
| 40.22 | 5.81 | 32.8 | 68.9 | 65.4 | |
| 20.40 | 3.19 | 36.1 | 47.2 | 30.1 |
1.2
| Modulus | Cadmium (Cd) | H |
Titanium (Ti) | Zirconium (Zr) | |
| 57.89 | 8.90 | 56.47 | 107.51 | 94.17 | |
| 48.61 | 8.90 | 56.37 | 107.50 | 94.02 | |
| 143.07 | 8.94 | 53.97 | 109.00 | 89.58 | |
| 20.95 | 8.82 | 61.86 | 104.63 | 104.36 |
It is not difficult to show that, in terms of our previous definitions
for the triaxial testing geometry, the coefficient 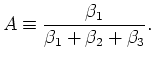 is given
precisely by the ratio
is given
precisely by the ratio
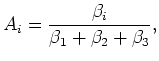 , so this contribution always
vanishes in (54). This fact explains why I did not
encounter this coefficient before in the analysis.
Note that there is no assumption here that the poroelastic system itself is
necessarily transversely isotropic. Only the prescribed equality of
the two applied transverse stresses,
, so this contribution always
vanishes in (54). This fact explains why I did not
encounter this coefficient before in the analysis.
Note that there is no assumption here that the poroelastic system itself is
necessarily transversely isotropic. Only the prescribed equality of
the two applied transverse stresses,
|
|
|
|
Poroelastic measurements resulting in complete data sets for granular and other anisotropic porous media |