 |
 |
 |
 | Poroelastic measurements resulting in complete data sets for granular
and other anisotropic porous media |  |
![[pdf]](icons/pdf.png) |
Next: Coefficient
Up: ANISOTROPIC POROELASTICITY
Previous: ANISOTROPIC POROELASTICITY
I will now provide several results for the 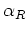 coefficients,
and then follow the results with a general proof of their correctness.
coefficients,
and then follow the results with a general proof of their correctness.
In many important and useful cases, the coefficients 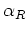 are determined by
are determined by
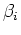 |
(28) |
Again, 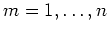 is the Reuss average of the grain modulus, since the local grain modulus
is not necessarily assumed uniform here as mentioned previously. Equation (28)
holds true for homogeneous grains, such that
is the Reuss average of the grain modulus, since the local grain modulus
is not necessarily assumed uniform here as mentioned previously. Equation (28)
holds true for homogeneous grains, such that
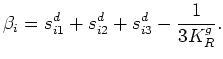 .
It also holds true for the case when
.
It also holds true for the case when 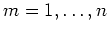 is determined instead by (6).
However, when the grains themselves are anisotropic, I need to allow again for this possibility,
and this can be accomplished by defining three directional grain bulk moduli determined by:
is determined instead by (6).
However, when the grains themselves are anisotropic, I need to allow again for this possibility,
and this can be accomplished by defining three directional grain bulk moduli determined by:
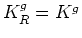 |
(29) |
for 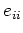 . The second equality follows because the compliance matrix is always symmetric.
I call these quantities in (29) the partial grain-compliance sums,
and the
. The second equality follows because the compliance matrix is always symmetric.
I call these quantities in (29) the partial grain-compliance sums,
and the
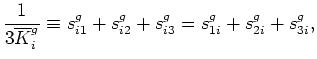 are the directional grain bulk moduli.
Then, the formula for (28) is replaced by
are the directional grain bulk moduli.
Then, the formula for (28) is replaced by
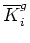 |
(30) |
Note that the factors of three have been correctly accounted for because
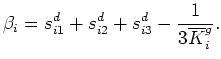 |
(31) |
in agreement with (8). If the three contributions represented by (29)
for 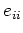 happen to be equal, then each equals one-third of the sum (31).
happen to be equal, then each equals one-third of the sum (31).
The preceding results are for perfectly aligned grains. If the grains are instead
perfectly randomly oriented, then it is clear that the formulas in (28) hold
as before, but now 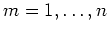 is determined instead by (8).
is determined instead by (8).
All of these statements about the 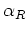 are easily proven by considering the
case when
are easily proven by considering the
case when
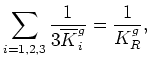 . In this situation,
from (22), I have:
. In this situation,
from (22), I have:
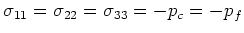 |
(32) |
in the most general of the three cases discussed, and holding true for each value of 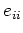 .
This is a statement about the strain
.
This is a statement about the strain 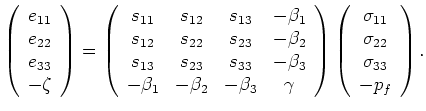 that would be observed in this situation, as it must be the same
if these anisotropic (or inhomogeneous) grains were immersed in the fluid, while measurements were taken
of the strains observed in each of the three directions
that would be observed in this situation, as it must be the same
if these anisotropic (or inhomogeneous) grains were immersed in the fluid, while measurements were taken
of the strains observed in each of the three directions 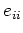 , during variations of the fluid pressure
, during variations of the fluid pressure 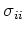 .
Consider this proof to be a thought experiment for determining the coefficients, in the same spirit as
those proposed originally by Biot and Willis
[see Stoll (1974); Biot and Willis (1957)] for the isotropic and homogeneous case.
.
Consider this proof to be a thought experiment for determining the coefficients, in the same spirit as
those proposed originally by Biot and Willis
[see Stoll (1974); Biot and Willis (1957)] for the isotropic and homogeneous case.
 |
 |
 |
 | Poroelastic measurements resulting in complete data sets for granular
and other anisotropic porous media |  |
![[pdf]](icons/pdf.png) |
Next: Coefficient
Up: ANISOTROPIC POROELASTICITY
Previous: ANISOTROPIC POROELASTICITY
2009-10-19
![]() coefficients,
and then follow the results with a general proof of their correctness.
coefficients,
and then follow the results with a general proof of their correctness.
![]() are determined by
are determined by
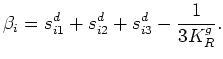 .
It also holds true for the case when
.
It also holds true for the case when 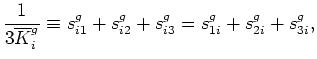 are the directional grain bulk moduli.
Then, the formula for (28) is replaced by
are the directional grain bulk moduli.
Then, the formula for (28) is replaced by
![]() is determined instead by (8).
is determined instead by (8).
![]() are easily proven by considering the
case when
are easily proven by considering the
case when
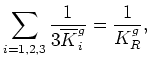 . In this situation,
from (22), I have:
. In this situation,
from (22), I have:
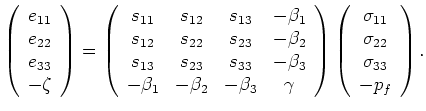 that would be observed in this situation, as it must be the same
if these anisotropic (or inhomogeneous) grains were immersed in the fluid, while measurements were taken
of the strains observed in each of the three directions
that would be observed in this situation, as it must be the same
if these anisotropic (or inhomogeneous) grains were immersed in the fluid, while measurements were taken
of the strains observed in each of the three directions