 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Example of Green's function
Up: De Ridder and Papanicolaou:
Previous: Green's function retrieval by
We proceed by studying the stationary phases of terms 15.6, 15.7, 15.10 and 15.11 in the iterated correlation. All terms correspond to particular combinations of ray paths.
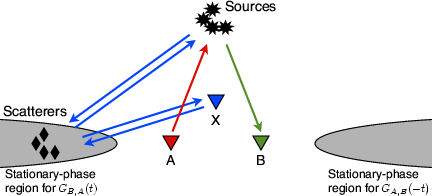
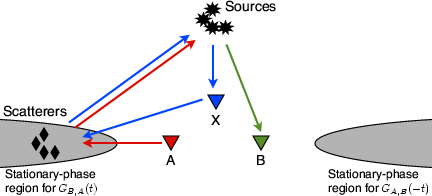
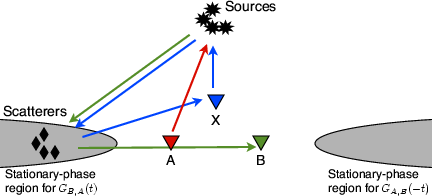
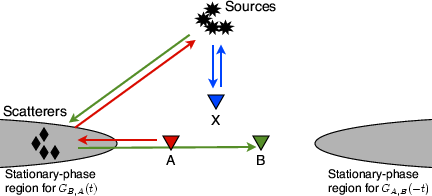
Figure 5 shows for each term a graphical illustration of the combination of ray paths. Ray paths towards the source are subtracted from the ray paths emitting from the source, as in the correlation process (a convolution of one Green's function with the time reverse of another Green's function).
The time domain of equation 15, including only the terms of group 2, is given as
where 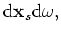 and
and 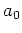 are amplitude factors. The rapid phases,
are amplitude factors. The rapid phases, 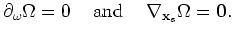 ,
, 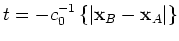 ,
, 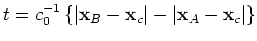 and
and 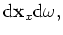 are found using equations A-6 and A-11; for a particular auxiliary station
are found using equations A-6 and A-11; for a particular auxiliary station
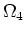 , we find
, we find
We analyze these rapid phases using the stationary-phase method, keeping
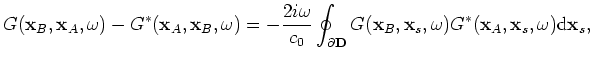 and
and
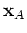 fixed and varying
fixed and varying
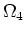 ,
,
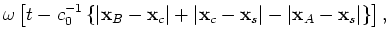 and
and
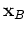 . According to the stationary-phase method, the dominant contribution to the integral and sum in equation 19 comes from positions of
. According to the stationary-phase method, the dominant contribution to the integral and sum in equation 19 comes from positions of
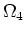 ,
,
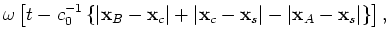 and
and
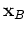 where
where
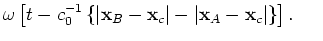 |
(49) |
From the rapid phase, 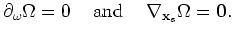 , of the first term in equation 19 we find stationary points for which
, of the first term in equation 19 we find stationary points for which
Conditions 27 and 28 are always satisfied. Condition 26 requires the stations to be on a line and the source to be on a line issuing from
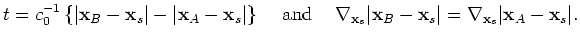 . When the stations and source are aligned as
. When the stations and source are aligned as
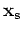 , condition 25 gives
, condition 25 gives
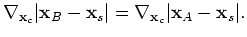 . When the stations and source are aligned as
. When the stations and source are aligned as
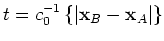 , the first condition gives
, the first condition gives
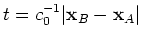 .
.
From the rapid phase, 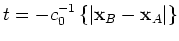 , of the first term in equation 19 we find stationary points for which
, of the first term in equation 19 we find stationary points for which
Condition 30 requires that station B, auxiliary station, the scatterer are on a line issuing from the source. Condition 31 requires that the auxiliary station and the scatterer are on a line issuing from the source. Condition 32 requires that station 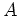 , an auxiliary station and a scatterer are on a line issuing from the source. In short, stations
, an auxiliary station and a scatterer are on a line issuing from the source. In short, stations 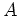 and
and 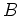 , an auxiliary station, and the scatterer all align on a line issuing from the source. When these are aligned as
, an auxiliary station, and the scatterer all align on a line issuing from the source. When these are aligned as
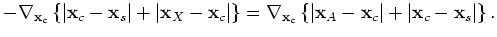 , then
, then
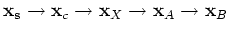 ,
,
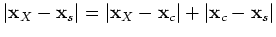 , and condition 29 gives
, and condition 29 gives
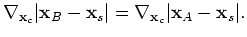 . When stations
. When stations  and
and  are reversed, condition 29 gives
are reversed, condition 29 gives
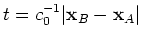 .
.
The rapid phase, 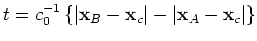 , of the third term in equation 19 is similar to the rapid phase,
, of the third term in equation 19 is similar to the rapid phase, 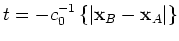 , of the second term in equation 19. If stations
, of the second term in equation 19. If stations 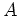 ,
, 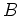 , an auxiliary station, and the scatterer are located on a line issuing from the source, aligned as
, an auxiliary station, and the scatterer are located on a line issuing from the source, aligned as
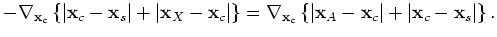 , the dominant contribution resides at
, the dominant contribution resides at
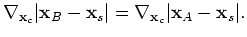 . When stations
. When stations 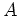 and
and 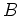 are interchanged, the dominant contribution of the third term in equation 19 resides at
are interchanged, the dominant contribution of the third term in equation 19 resides at
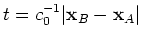 .
Last we analyze the rapid phase,
.
Last we analyze the rapid phase, 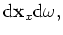 , of the fourth term in equation 19, and we find stationary points for which
, of the fourth term in equation 19, and we find stationary points for which
Conditions 34 and 35 are always satisfied. Condition 36 is satisfied when the scatterer lies on a line through stations 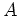 and
and 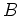 . When stations
. When stations 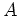 ,
, 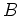 and the scatterer are aligned as
and the scatterer are aligned as
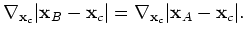 , condition 33 gives
, condition 33 gives
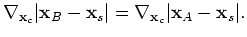 . When stations
. When stations 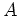 ,
, 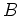 and the scatterer align as
and the scatterer align as
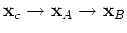 , condition 33 gives
, condition 33 gives
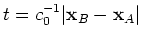 .
.
 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Example of Green's function
Up: De Ridder and Papanicolaou:
Previous: Green's function retrieval by
2009-05-05
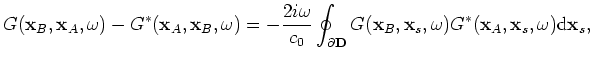 and
and
![]() , of the first term in equation 19 we find stationary points for which
, of the first term in equation 19 we find stationary points for which
![]() , of the first term in equation 19 we find stationary points for which
, of the first term in equation 19 we find stationary points for which
![]() , of the third term in equation 19 is similar to the rapid phase,
, of the third term in equation 19 is similar to the rapid phase, ![]() , of the second term in equation 19. If stations
, of the second term in equation 19. If stations ![]() ,
, ![]() , an auxiliary station, and the scatterer are located on a line issuing from the source, aligned as
, an auxiliary station, and the scatterer are located on a line issuing from the source, aligned as
![]() , the dominant contribution resides at
, the dominant contribution resides at
![]() . When stations
. When stations ![]() and
and ![]() are interchanged, the dominant contribution of the third term in equation 19 resides at
are interchanged, the dominant contribution of the third term in equation 19 resides at
![]() .
Last we analyze the rapid phase,
.
Last we analyze the rapid phase, ![]() , of the fourth term in equation 19, and we find stationary points for which
, of the fourth term in equation 19, and we find stationary points for which