 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Stationary phases in iterated
Up: De Ridder and Papanicolaou:
Previous: Example of Green's function
In the absence of complete source coverage, we can make use of the scattering properties of the medium to mitigate the directivity of the wave field.
The iterated correlation between stations 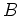 and
and 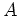 is defined using auxiliary station X as follows:
is defined using auxiliary station X as follows:
The Green's function in the Born approximation for a scattering medium is composed of two terms;
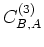 therefore contains
therefore contains 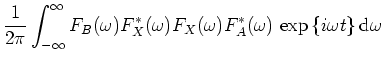 terms
terms
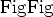 |
|
|
(21) |
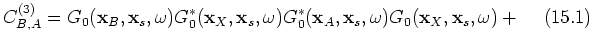 |
|
|
(22) |
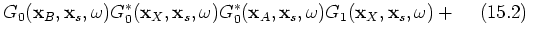 |
|
|
(23) |
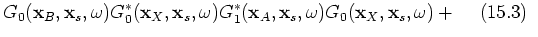 |
|
|
(24) |
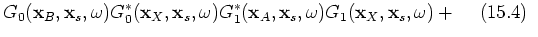 |
|
|
(25) |
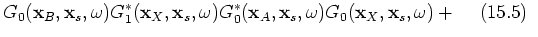 |
|
|
(26) |
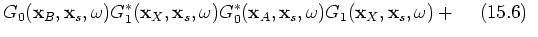 |
|
|
(27) |
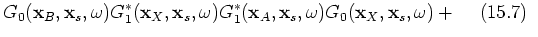 |
|
|
(28) |
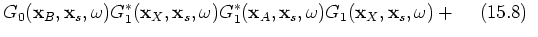 |
|
|
(29) |
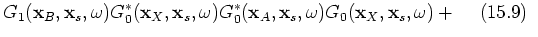 |
|
|
(30) |
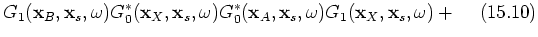 |
|
|
(31) |
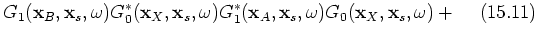 |
|
|
(32) |
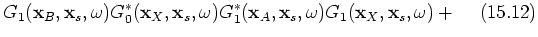 |
|
|
(33) |
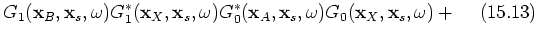 |
|
|
(34) |
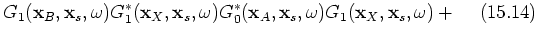 |
|
|
(35) |
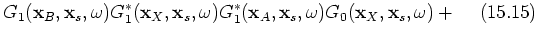 |
|
|
(36) |
Three groups of terms can be distinguished; group 1 includes terms 15.1, 15.2, 15.3, 15.4, 15.5, 15.9 and 15.13, which are terms correlating with the dominant contribution in 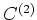 ;
; 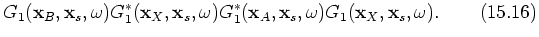 . Group 2 contains the terms of interest in this paper; 15.6, 15.7, 15.10 and 15.11; see the stationary-phase analysis below. The third group contains events that are of order
. Group 2 contains the terms of interest in this paper; 15.6, 15.7, 15.10 and 15.11; see the stationary-phase analysis below. The third group contains events that are of order 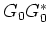 and includes terms 15.8, 15.12, 15.14, 15.15 and 15.16. The leading term in
and includes terms 15.8, 15.12, 15.14, 15.15 and 15.16. The leading term in 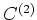 contributes to a spurious term, because the source is not located at a stationary angle of the event between stations A and B. To exclude the terms of group 1, we remove the dominant term after forming
contributes to a spurious term, because the source is not located at a stationary angle of the event between stations A and B. To exclude the terms of group 1, we remove the dominant term after forming
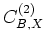 and
and
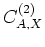 . This is done by muting the correlation in the time domain to suppress all times smaller than
. This is done by muting the correlation in the time domain to suppress all times smaller than
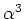 :
:
where
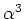 is defined as an estimated traveltime between the main stations and the auxiliary stations,
is defined as an estimated traveltime between the main stations and the auxiliary stations,
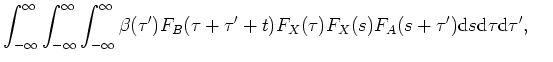 is a muting function that is zero for
is a muting function that is zero for
![$ \beta(\tau)=0 \mathrm{for} \tau : [-\tau_{coda} : \tau_{coda}]$](img123.png) and otherwise
and otherwise
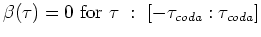 .
.
We learned from Figure 3 that the dominant term always arrives within that time window. We average the iterated correlations over a network of  auxiliary stations and include a phase-modifying term,
auxiliary stations and include a phase-modifying term,
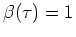 |
(39) |
where
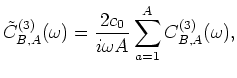 is an implicit function of auxiliary-station position
is an implicit function of auxiliary-station position
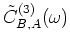 , according to equation 15. The phase-modifying proportionality factor is chosen such that the
, according to equation 15. The phase-modifying proportionality factor is chosen such that the
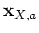 factor in the Born approximation (see equation A-10) is matched to the
factor in the Born approximation (see equation A-10) is matched to the
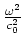 factor in conventional interferometry (equation 2).
factor in conventional interferometry (equation 2).
 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Stationary phases in iterated
Up: De Ridder and Papanicolaou:
Previous: Example of Green's function
2009-05-05
![]() therefore contains
therefore contains 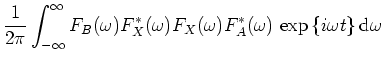 terms
terms
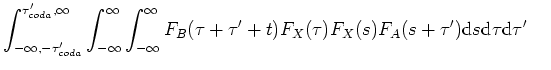
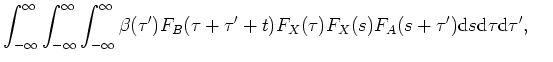 is a muting function that is zero for
is a muting function that is zero for
![]() auxiliary stations and include a phase-modifying term,
auxiliary stations and include a phase-modifying term,
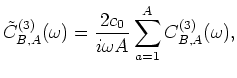 is an implicit function of auxiliary-station position
is an implicit function of auxiliary-station position