 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Wave equation and Green's
Previous: Frequency-domain Green's function in
We are interested in the Green's function in an inhomogeneous medium. We assume the velocity can be split into a background velocity 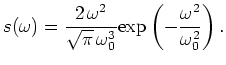 and a perturbation
and a perturbation
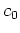 as
as
![$ c^{-2}(\mathbf{x}) = c^{-2}_0\left[ 1+ \alpha(\mathbf{x})\right]$](img200.png) . Assuming the perturbation is confined inside some finite domain
. Assuming the perturbation is confined inside some finite domain
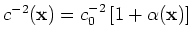 , the Green's function in the Born approximation can now be computed in terms of a Green's function computed in the background,
, the Green's function in the Born approximation can now be computed in terms of a Green's function computed in the background, 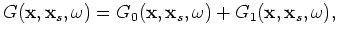 , medium as
, medium as
The Green's function in the background medium is computed using equation A-5 with 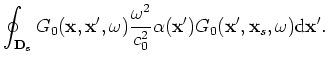 . When the medium consists of a homogeneous background with a series of
. When the medium consists of a homogeneous background with a series of 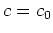 scatters positioned at
scatters positioned at
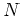 with strength
with strength
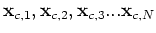 , then
, then
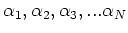 . Hence the Green's function
. Hence the Green's function 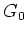 in equation A-10 can be written as
in equation A-10 can be written as
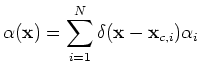 |
(72) |
 |
 |
 |
 | Kinematics in iterated correlations of a passive acoustic experiment |  |
![[pdf]](icons/pdf.png) |
Next: Bibliography
Up: Wave equation and Green's
Previous: Frequency-domain Green's function in
2009-05-05
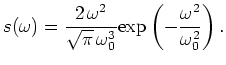 and a perturbation
and a perturbation
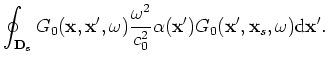 . When the medium consists of a homogeneous background with a series of
. When the medium consists of a homogeneous background with a series of ![]() scatters positioned at
scatters positioned at
![]() with strength
with strength
![]() , then
, then
![]() . Hence the Green's function
. Hence the Green's function ![]() in equation A-10 can be written as
in equation A-10 can be written as