




Next: Synthetic and field data
Up: Coherent noise filtering and
Previous: The modeling approach
The filtering approach for coherent noise removal can lead to
a covariance-pattern based approach. This technique is often
called pattern-based approach for short.
The basic idea is to separate the noise and signal present in the data
according to their pattern, or multivariate spectra. To identify and
approximate these patterns, multidimensional PEFs can be used.
I now show briefly how this technique works. Building on equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we introduce a regularization operator to obtain
) we introduce a regularization operator to obtain
| 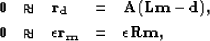 |
(28) |
and minimize
| 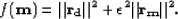 |
(29) |
In this case,  is a trade-off parameter between data fitting
and model smoothing. In the pattern-based approach, the unknown
parameter is the signal
is a trade-off parameter between data fitting
and model smoothing. In the pattern-based approach, the unknown
parameter is the signal 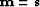 and the modeling operator
and the modeling operator
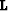 becomes the identity. This choice of
becomes the identity. This choice of 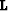 comes from
the fact that both the signal and the noise reside simultaneously
in the data space. In the filtering approach,
comes from
the fact that both the signal and the noise reside simultaneously
in the data space. In the filtering approach, 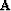 is a PEF that
annihilates the noise components. Let us call it
is a PEF that
annihilates the noise components. Let us call it 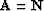 . For
the regularization operator, we need to find an operator for the
signal such that
. For
the regularization operator, we need to find an operator for the
signal such that 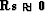 . By definition, a PEF
. By definition, a PEF  that annihilates the signal components is a good candidate for
that annihilates the signal components is a good candidate for 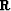 . From these choices, we end up with
. From these choices, we end up with
| 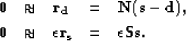 |
(30) |
Solving equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in a least-squares sense gives for
the estimated signal Abma (1995):
) in a least-squares sense gives for
the estimated signal Abma (1995):
| 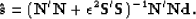 |
(31) |
Note that 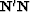 and
and 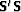 are the inverse multidimensional
spectra for the noise and signal, respectively, which explains why
this technique of signal/noise separation is called pattern-based.
As stated by Claerbout and Fomel (2000), PEFs are important
where they are small. Analyzing the noise filter in equation (
are the inverse multidimensional
spectra for the noise and signal, respectively, which explains why
this technique of signal/noise separation is called pattern-based.
As stated by Claerbout and Fomel (2000), PEFs are important
where they are small. Analyzing the noise filter in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
| 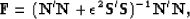 |
(32) |
we see that
| 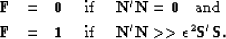 |
(33) |
The first condition is met when the noise is strong (PEF 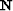 small), thus attenuating the noise, and the second when the signal is
strong (PEF
small), thus attenuating the noise, and the second when the signal is
strong (PEF  small), thus preserving it. The filter
small), thus preserving it. The filter 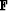 is also a projection filter Sacchi and Kuehl (2001); Soubaras (1994).
is also a projection filter Sacchi and Kuehl (2001); Soubaras (1994).
In the pattern-based approach, 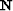 and
and  need to be
estimated before the actual separation. This is the main challenge of
this technique, i.e, how to choose good noise and signal models.
Chapter
need to be
estimated before the actual separation. This is the main challenge of
this technique, i.e, how to choose good noise and signal models.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrate
the pattern-based technique for surface-related multiple attenuation.
In this case, strategies exist to estimate the noise and signal PEFs.
In the next section, I illustrate the filtering and modeling
techniques on synthetic and field data examples.
illustrate
the pattern-based technique for surface-related multiple attenuation.
In this case, strategies exist to estimate the noise and signal PEFs.
In the next section, I illustrate the filtering and modeling
techniques on synthetic and field data examples.





Next: Synthetic and field data
Up: Coherent noise filtering and
Previous: The modeling approach
Stanford Exploration Project
5/5/2005
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we introduce a regularization operator to obtain
) we introduce a regularization operator to obtain
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) we introduce a regularization operator to obtain
) we introduce a regularization operator to obtain
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) in a least-squares sense gives for
the estimated signal Abma (1995):
) in a least-squares sense gives for
the estimated signal Abma (1995):
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) )
)
![]() and
and ![]() need to be
estimated before the actual separation. This is the main challenge of
this technique, i.e, how to choose good noise and signal models.
Chapter
need to be
estimated before the actual separation. This is the main challenge of
this technique, i.e, how to choose good noise and signal models.
Chapter ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) illustrate
the pattern-based technique for surface-related multiple attenuation.
In this case, strategies exist to estimate the noise and signal PEFs.
In the next section, I illustrate the filtering and modeling
techniques on synthetic and field data examples.
illustrate
the pattern-based technique for surface-related multiple attenuation.
In this case, strategies exist to estimate the noise and signal PEFs.
In the next section, I illustrate the filtering and modeling
techniques on synthetic and field data examples.