




Next: The modeling approach
Up: Noise attenuation by filtering
Previous: A modeling approach
The core of the filtering method is the PEF 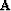 that
destroys the coherent noise present in the residual. In order to
accommodate the possible complexity in space and time of the
undesirable events, these filters can have any dimensions thanks to
the helical boundary conditions
Claerbout (1998); Mersereau and Dudgeon (1974). In addition, these filters
can be made non-stationary in any directions
Claerbout and Fomel (2002); Crawley (2000); Margrave (1998). Chapters
that
destroys the coherent noise present in the residual. In order to
accommodate the possible complexity in space and time of the
undesirable events, these filters can have any dimensions thanks to
the helical boundary conditions
Claerbout (1998); Mersereau and Dudgeon (1974). In addition, these filters
can be made non-stationary in any directions
Claerbout and Fomel (2002); Crawley (2000); Margrave (1998). Chapters ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) will illustrate these possibilities.
will illustrate these possibilities.
If a noise model is known in advance, a PEF can be estimated from it
and used directly for the inversion of  in equation
(
in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
 :
:
- 1.
- Set
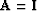 and
and 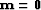 .
. - 2.
- Iterate until the data residual
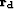 contains mostly coherent noise.
contains mostly coherent noise.
- 3.
- Estimate a new PEF
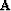 from the residual.
from the residual.
- 4.
- Set
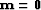 and iterate.
and iterate.
- 5.
- Inspect the residual. If white then stop else reestimate the
PEF
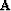 from the unweighted residual
from the unweighted residual 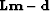 and go
to (4).
and go
to (4).
This nonlinear process tries to refine the PEF estimation by
bootstrapping in order to obtain the best possible coherent
noise filter  Clapp (2003).
It is also based on the assumption that the coherent noise
will stay in the residual after a certain number of iterations.
Therefore, the residual needs to be closely watched at
each iteration, which requires a certain level of human interpretation.
Clapp (2003).
It is also based on the assumption that the coherent noise
will stay in the residual after a certain number of iterations.
Therefore, the residual needs to be closely watched at
each iteration, which requires a certain level of human interpretation.
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) and
and ![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) will illustrate these possibilities.
will illustrate these possibilities.
![]() in equation
(
in equation
(![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
). If a noise model is not known in advance,
I propose the following algorithm based on the iterative inversion of
![]() :
: