




Next: A modeling approach
Up: Proposed solutions to attenuate
Previous: Proposed solutions to attenuate
The filtering method is motivated by the need for estimating the noise
covariance operator when the data are noisy. The noise covariance
operator has deep theoretical roots for least-squares estimation
but its estimation remains somewhat obscure
or difficult to achieve. This is why in practice,
this matrix is approximated with diagonal operators.
In this section I give a method that computes
non-diagonal covariance matrices using prediction-error filters.
When coherent noise is present in the data, residual variables
are no longer IID. The coherent noise will add ``color''
to the spectrum of the residual. The key idea is to recognize that
the goal of the inverse covariance matrix 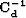 is to absorb this spectrum. Now, as Claerbout and Fomel (2002) assert:
is to absorb this spectrum. Now, as Claerbout and Fomel (2002) assert:
Clearly, the noise spectrum is the same as the data covariance only if
we accept the theoretician's definition that E(d)=Fm.
There is no ambiguity and no argument if we drop the word ``variance''
and use the word ``spectrum''.
This statement is the basis of the filtering method.
It says that the data residuals (squared) should be
weighted by their inverse multivariate spectrum for
optimal convergence. Because a prediction-error filter (PEF)
whitens data from which it was estimated Burg (1975),
it approximates the inverse power spectrum. Thus a PEF (squared)
with the inverse spectrum of the coherent noise accomplishes the role
of the inverse covariance matrix 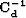 in equation (
in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The fitting goals in equation (
).
The fitting goals in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) become, omitting
the regularization term,
) become, omitting
the regularization term,
| 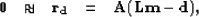 |
(19) |
where 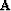 is a PEF that whitens the coherent noise.
Therefore, the noise covariance matrix is approximated as follows:
is a PEF that whitens the coherent noise.
Therefore, the noise covariance matrix is approximated as follows:
| 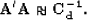 |
(20) |
This method is solely based on the whitening properties of the PEFs;
other types of filters can be used as well. The next section
introduces a noise modeling approach. I show that this method reduces
to a weighting of the residual with a projection filter.





Next: A modeling approach
Up: Proposed solutions to attenuate
Previous: Proposed solutions to attenuate
Stanford Exploration Project
5/5/2005
![]() is to absorb this spectrum. Now, as Claerbout and Fomel (2002) assert:
is to absorb this spectrum. Now, as Claerbout and Fomel (2002) assert:
![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ).
The fitting goals in equation (
).
The fitting goals in equation (![[*]](http://sepwww.stanford.edu/latex2html/cross_ref_motif.gif) ) become, omitting
the regularization term,
) become, omitting
the regularization term,