




Next: Full-model for
Up: Patchy-Saturation Transport
Previous: Low-frequency limit of
It has already been commented that in the extreme high-frequency limit
where each patch behaves as if it were sealed to flow (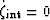 ),
the theory of Hill (1963) applies. Hill demonstrated, among other things,
that when each isotropic patch has the same shear modulus, the volumetric
deformation within each patch is a spatial constant. The fluid
pressure response in this limit
),
the theory of Hill (1963) applies. Hill demonstrated, among other things,
that when each isotropic patch has the same shear modulus, the volumetric
deformation within each patch is a spatial constant. The fluid
pressure response in this limit 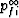 is thus a uniform spatial
constant throughout each phase except in a vanishingly small neighborhood of the
interface
is thus a uniform spatial
constant throughout each phase except in a vanishingly small neighborhood of the
interface 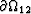 where equilibration is attempting to
take place. The small amount of fluid-pressure
penetration that is occuring across
where equilibration is attempting to
take place. The small amount of fluid-pressure
penetration that is occuring across 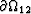 can be locally modeled as
a one-dimensional process normal to the interface.
can be locally modeled as
a one-dimensional process normal to the interface.
Using the coordinate x to measure linear distance normal to the interface (and
into phase 1),
one has that equation (56) is satisfied by
| 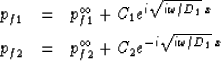 |
(72) |
| (73) |
where the diffusivities are defined 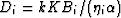 .The constants Ci are found from the continuity conditions (57)
to be
.The constants Ci are found from the continuity conditions (57)
to be
| 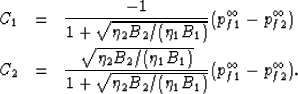 |
(74) |
| (75) |
Although not actually needed here, we have that 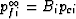 where the uniform confining pressure of each patch is given by equations
(40) and (41) so that the fluid pressure difference between the
phases goes as
where the uniform confining pressure of each patch is given by equations
(40) and (41) so that the fluid pressure difference between the
phases goes as
| 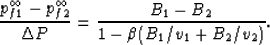 |
(76) |
This equation is exactly the difference between equations (50) and
(51).
Because the penetration distance 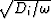 vanishes at high-frequencies,
we may state that to leading order in the high-frequency
limit,
vanishes at high-frequencies,
we may state that to leading order in the high-frequency
limit, 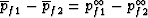 .
.
To obtain the high-frequency limit of the transport coefficient 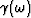 ,
we use the definition (53) of the internal transport (note
that
,
we use the definition (53) of the internal transport (note
that 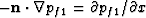 )
)
| 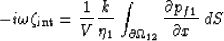 |
(77) |
along with equations (72) and (74). The result is
| 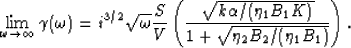 |
(78) |
Here, S is again the area of 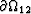 contained within
a volume V of the patchy composite.
contained within
a volume V of the patchy composite.





Next: Full-model for
Up: Patchy-Saturation Transport
Previous: Low-frequency limit of
Stanford Exploration Project
10/14/2003
![]() ),
the theory of Hill (1963) applies. Hill demonstrated, among other things,
that when each isotropic patch has the same shear modulus, the volumetric
deformation within each patch is a spatial constant. The fluid
pressure response in this limit
),
the theory of Hill (1963) applies. Hill demonstrated, among other things,
that when each isotropic patch has the same shear modulus, the volumetric
deformation within each patch is a spatial constant. The fluid
pressure response in this limit ![]() is thus a uniform spatial
constant throughout each phase except in a vanishingly small neighborhood of the
interface
is thus a uniform spatial
constant throughout each phase except in a vanishingly small neighborhood of the
interface ![]() where equilibration is attempting to
take place. The small amount of fluid-pressure
penetration that is occuring across
where equilibration is attempting to
take place. The small amount of fluid-pressure
penetration that is occuring across ![]() can be locally modeled as
a one-dimensional process normal to the interface.
can be locally modeled as
a one-dimensional process normal to the interface.
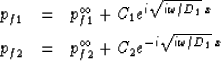
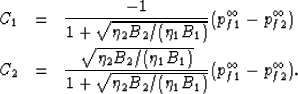
![]() ,
we use the definition (53) of the internal transport (note
that
,
we use the definition (53) of the internal transport (note
that ![]() )
)