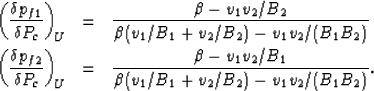Next: Patchy-Saturation Transport
Up: PATCHY-SATURATION MODEL
Previous: PATCHY-SATURATION MODEL
To obtain the aij for the patchy-saturation model, we note that
each patch has the same  and K. The poroelastic
differences between patches is entirely due to B1 being different
than B2. Upon volume averaging equation (3)
and using
and K. The poroelastic
differences between patches is entirely due to B1 being different
than B2. Upon volume averaging equation (3)
and using 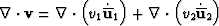 ,
where an overline again denotes a volume average over
the appropriate phase, and using the fact that the aij are defined
in the extreme high-frequency limit where
the fluids have no time to traverse the internal
interface
,
where an overline again denotes a volume average over
the appropriate phase, and using the fact that the aij are defined
in the extreme high-frequency limit where
the fluids have no time to traverse the internal
interface 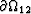 (i.e., the aij are
defined under the condition that
(i.e., the aij are
defined under the condition that 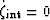 ),
one has
),
one has
| 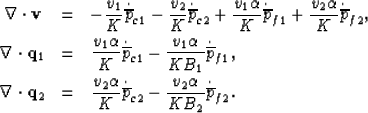 |
(37) |
| (38) |
| (39) |
The average confining pressures 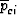 in each phase are not
a priori known; however, they are necessarily linear functions
of the three independent applied pressures of the theory
in each phase are not
a priori known; however, they are necessarily linear functions
of the three independent applied pressures of the theory
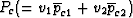 ,
,
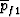 , and
, and 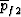 . It is straightforward
to demonstrate that if and only if the average confining pressures
take the form
. It is straightforward
to demonstrate that if and only if the average confining pressures
take the form
| 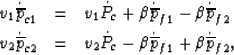 |
(40) |
| (41) |
will equations (37)-(39) produce aij that
satisfy the thermodynamic symmetry requirement of
aij = aji [i.e., these aij constants are all second
derivatives of a strain-energy function as demonstrated by
Pride and Berryman (2003a). Upon placing equations
(40) and (41) into equations (37)-(39), we then have
| 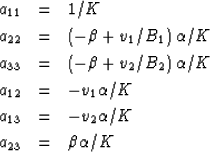 |
(42) |
| (43) |
| (44) |
| (45) |
| (46) |
| (47) |
where 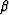 is a constant to be determined.
is a constant to be determined.
To obtain 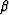 , we note that in the high-frequency limit,
each local patch of phase i
is undrained and thus
characterized by an undrained bulk modulus
, we note that in the high-frequency limit,
each local patch of phase i
is undrained and thus
characterized by an undrained bulk modulus 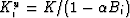 and
a shear modulus G that is the same for all patches. In this limit,
the usual laws of elasticity govern the response of this heterogeneous
composite. Under these precise conditions (elasticity of an isotropic
composite having uniform G and all heterogeneity confined
to the bulk modulus which in the present case corresponds to Kiu),
the theorem of Hill (1963)
applies, which states that the overall
undrained-unrelaxed modulus of the composite KH is given exactly by
and
a shear modulus G that is the same for all patches. In this limit,
the usual laws of elasticity govern the response of this heterogeneous
composite. Under these precise conditions (elasticity of an isotropic
composite having uniform G and all heterogeneity confined
to the bulk modulus which in the present case corresponds to Kiu),
the theorem of Hill (1963)
applies, which states that the overall
undrained-unrelaxed modulus of the composite KH is given exactly by
| 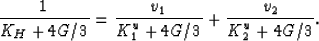 |
(48) |
In terms of the
aij, this same undrained-unrelaxed Hill modulus is given by
| 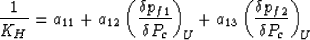 |
(49) |
where, upon using 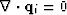 and
and 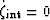 in equation (8) and then using (42)-(47),
the undrained-unrelaxed pressure ratios are
in equation (8) and then using (42)-(47),
the undrained-unrelaxed pressure ratios are
| 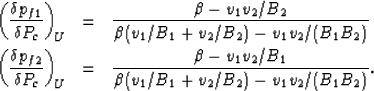 |
(50) |
| (51) |
Thus, after some algebra, equation (49) yields the exact result
| ![\begin{displaymath}
\beta =v_1 v_2 \!\!\left(\frac{v_1 }{ B_2}+\frac{v_2}{B_1}\r...
...v_2 B_2)}
{\alpha - (1 - K/K_{H})(v_1/ B_1 + v_2/ B_2)}
\right]\end{displaymath}](img81.gif) |
(52) |
with KH given by equation (48). All
the aij are now expressed in terms of known information.





Next: Patchy-Saturation Transport
Up: PATCHY-SATURATION MODEL
Previous: PATCHY-SATURATION MODEL
Stanford Exploration Project
10/14/2003
![]() and K. The poroelastic
differences between patches is entirely due to B1 being different
than B2. Upon volume averaging equation (3)
and using
and K. The poroelastic
differences between patches is entirely due to B1 being different
than B2. Upon volume averaging equation (3)
and using ![]() ,
where an overline again denotes a volume average over
the appropriate phase, and using the fact that the aij are defined
in the extreme high-frequency limit where
the fluids have no time to traverse the internal
interface
,
where an overline again denotes a volume average over
the appropriate phase, and using the fact that the aij are defined
in the extreme high-frequency limit where
the fluids have no time to traverse the internal
interface ![]() (i.e., the aij are
defined under the condition that
(i.e., the aij are
defined under the condition that ![]() ),
one has
),
one has
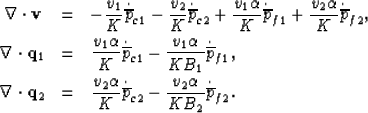
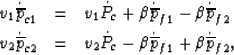
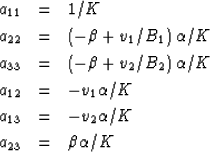
![]() , we note that in the high-frequency limit,
each local patch of phase i
is undrained and thus
characterized by an undrained bulk modulus
, we note that in the high-frequency limit,
each local patch of phase i
is undrained and thus
characterized by an undrained bulk modulus ![]() and
a shear modulus G that is the same for all patches. In this limit,
the usual laws of elasticity govern the response of this heterogeneous
composite. Under these precise conditions (elasticity of an isotropic
composite having uniform G and all heterogeneity confined
to the bulk modulus which in the present case corresponds to Kiu),
the theorem of Hill (1963)
applies, which states that the overall
undrained-unrelaxed modulus of the composite KH is given exactly by
and
a shear modulus G that is the same for all patches. In this limit,
the usual laws of elasticity govern the response of this heterogeneous
composite. Under these precise conditions (elasticity of an isotropic
composite having uniform G and all heterogeneity confined
to the bulk modulus which in the present case corresponds to Kiu),
the theorem of Hill (1963)
applies, which states that the overall
undrained-unrelaxed modulus of the composite KH is given exactly by