




Next: High-frequency limit of
Up: Patchy-Saturation Transport
Previous: Mesoscopic flow equations
As 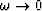 , one can represent the local fields as
asymptotic series in the small parameter
, one can represent the local fields as
asymptotic series in the small parameter 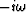
| 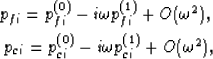 |
(60) |
| (61) |
and equivalently for 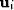 .
The zeroth-order response corresponds to uniform
fluid pressure in the pores and is therfore given by
.
The zeroth-order response corresponds to uniform
fluid pressure in the pores and is therfore given by 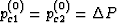 and
and
| 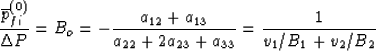 |
(62) |
where the patchy-saturation aij have been employed.
The fact that the quasi-static Skempton's coefficient in the patchy-saturation
model is exactly the harmonic average of the constituents Bi is equivalent to
saying that at low frequencies, the fluid bulk modulus is given by
1/Kf = v1 /Kf1 + v2 /Kf2. The quasi-static response is
thus completely independent of the spatial geometry of the fluid patches; it depends
only on the volume fractions occupied by the patches.
The leading order correction to uniform fluid pressure is then controlled by
the boundary-value problem
| 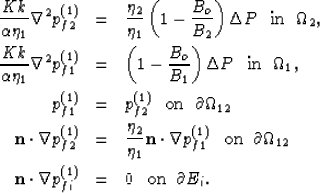 |
(63) |
| (64) |
| (65) |
| (66) |
| (67) |
It is now assumed that for patchy-saturation
cases of interest (air/water or water/oil), the ratio 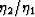 can be considered small.
To leading order in
can be considered small.
To leading order in 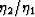 , equations (63), (66), and (67)
require that
, equations (63), (66), and (67)
require that 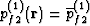 (a spatial constant).
The fluid pressure in phase 1 is now rewritten as
(a spatial constant).
The fluid pressure in phase 1 is now rewritten as
| 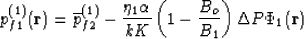 |
(68) |
where, from equations (64), (65) and (67) and
to leading order in 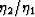 , the potential
, the potential 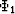 is the solution of
the same elliptic boundary-value problem (25)-(27)
given earlier.
is the solution of
the same elliptic boundary-value problem (25)-(27)
given earlier.
Upon averaging (68) over all of 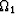 , the
leading order in
, the
leading order in 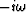 difference in the average fluid pressures can be written
difference in the average fluid pressures can be written
| 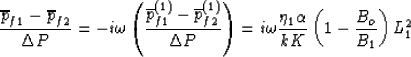 |
(69) |
where L1 is again the length defined by equation (24).
To connect this fluid-pressure difference to the increment 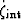 we use
the divergence theorem and the no-flow boundary condition on
we use
the divergence theorem and the no-flow boundary condition on
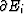 to write equation (53) as
to write equation (53) as
| 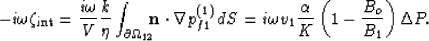 |
(70) |
Replacing 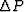 with
with 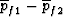 using equation (69)
then gives the desired law
using equation (69)
then gives the desired law
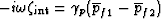 with
with
| ![\begin{displaymath}
\gamma_p = \frac{v_1 k}{\eta_1 L_1^2} \left[1 + O\left(\frac{\eta_2}{\eta_1}\right)\right].\end{displaymath}](img126.gif) |
(71) |
being the low-frequency limit of interest.





Next: High-frequency limit of
Up: Patchy-Saturation Transport
Previous: Mesoscopic flow equations
Stanford Exploration Project
10/14/2003
![]() , one can represent the local fields as
asymptotic series in the small parameter
, one can represent the local fields as
asymptotic series in the small parameter ![]()
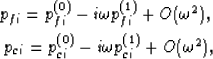
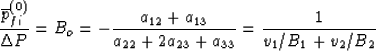
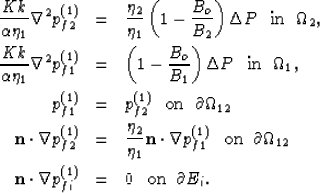
![]() , the
leading order in
, the
leading order in ![]() difference in the average fluid pressures can be written
difference in the average fluid pressures can be written
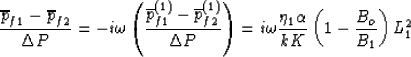
![]() we use
the divergence theorem and the no-flow boundary condition on
we use
the divergence theorem and the no-flow boundary condition on
![]() to write equation (53) as
to write equation (53) as