Patchy-Saturation Transport

We next must address the internal fluid-pressure equilibration between the two phases with the goal of obtaining the internal transfer coefficient 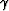$\gamma$ of equation (9). The mathematical definition of the rate of internal fluid transfer is  

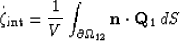$$\dot{\zeta}_{\rm int} = \frac{1}{V} \int_{\partial \Omega_{12}} {\bf n} \cdot {\bf Q}_1 \, dS$$ (53)

where V is the volume occupied by the composite. A possible concern in the patchy-saturation analysis is whether capillary effects at the local interface 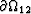$\partial \Omega_{12}$ separating the two phases need to be allowed for.

 

• Local continuity conditions on $\partial \Omega_{12}$
• Mesoscopic flow equations
• Low-frequency limit of $\gamma(\omega)$
• High-frequency limit of $\gamma(\omega)$
• Full-model for $\gamma(\omega)$